题目内容
10.已知函数f(x)的定义域为A,若其值域也为A,则称区间A为f(x)的保值区间,若f(x)=x+m-lnx的保值区间是(e,+∞),则m的值为1.分析 利用导数求出函数f(x)的单调区间,结合f(x)=x+m-lnx的保值区间是(e,+∞),可得其定义域和值域均为(e,+∞),由此列式求得m值.
解答 解:∵f′(x)=1-$\frac{1}{x}$>0,得x>1,
∴f(x)在(1,+∞)上为增函数,同理可得f(x)在(0,1)上为减函数.
又∵f(x)=x+m-lnx的保值区间是[e,+∞),则定义域为[e,+∞),
∴函数f(x)在[e,+∞)上单调递增,
且f(x)min=f(e)=e+m-1=e,
∴m=1.
故答案为:1.
点评 本题考查函数的值域,训练了利用导数研究函数的单调性,关键是对题意的理解,是中档题.

练习册系列答案
相关题目
2.已知函数f(x)=xa的图象过点(4,2),令an=$\frac{1}{f(n+1)+f(n)}$,n∈N*,记数列{an}的前n项和为Sn,则S2014=( )
| A. | $\sqrt{2013}$-1 | B. | $\sqrt{2014}$-1 | C. | $\sqrt{2015}$-1 | D. | $\sqrt{2015}$+1 |
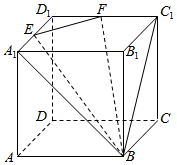 如图,已知正方体ABCD-A1B1C1D1的边长为2,点E,F分别是A1D1,C1D1的中点.
如图,已知正方体ABCD-A1B1C1D1的边长为2,点E,F分别是A1D1,C1D1的中点.