Question

  某营养师要为某个儿童预定午餐和晚餐。已知一个单位的午餐含12个单位的碳水化合物6个单位蛋白质和6个单位的维生素C；一个单位的晚餐含8个单位的碳水化合物，6个单位的蛋白质和10个单位的维生素C.另外，该儿童这两餐需要的营养中至少含64个单位的碳水化合物，42个单位的蛋白质和54个单位的维生素C. 如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预定多少个单位的午餐和晚餐？

Answer 1

19．解：设应当为该儿童分别预订个单位的午餐，个单位的晚餐，所花的费用为，则依题意得：

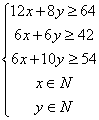        满足条件即，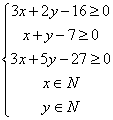

        目标函数为，

   作出二元一次不等式组所表示的平面区域（图略），把变形为，得到斜率为，在轴上的截距为，随变化的一族平行直线。

 由图可知，当直线经过可行域上的点M时截距最小，即最小.

       解方程组：, 得点M的坐标为, 所以22

答：要满足营养要求，并花费最少，应当为该儿童分别预订4个单位的午餐，3个单位的晚餐，

所花的费用最少,且最少费用为22元.