题目内容
在 的值是( )
的值是( )A.

B.

C.
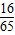 或
或
D.以上都不对
【答案】分析:通过sinA,求cos的值,再通过∠A+∠B+∠C=180°的关系,使cosC=-cos(A+B),再利用两角和公式,得出答案.
解答:解:∵sinA= ,cosB=
,cosB=
∴cosA= =
= =±
=± ,sinB=
,sinB=
∵依题意sinA>cosB,∴A+B>90°
又∵sinB>sinA,∴A<90°,∴cosA=
∴cosC=-cos(A+B)=sinAsinB-cosAcosB= ×
× -
- ×
× =
=
故选B
点评:本题主要考查预先函数的两角和与差的问题.关键是利用了三角形内角的和为180°.
解答:解:∵sinA=
 ,cosB=
,cosB=
∴cosA=
 =
= =±
=± ,sinB=
,sinB=
∵依题意sinA>cosB,∴A+B>90°
又∵sinB>sinA,∴A<90°,∴cosA=

∴cosC=-cos(A+B)=sinAsinB-cosAcosB=
 ×
× -
- ×
× =
=
故选B
点评:本题主要考查预先函数的两角和与差的问题.关键是利用了三角形内角的和为180°.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 的值是( )
的值是( )

 或
或
 的值是( )
的值是( )

 或
或
 的值是( )
的值是( )

 或
或
 的值是( )
的值是( )

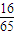 或
或