题目内容
设函数f(x)= ·
· ,其中向量
,其中向量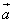 =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx, sin2x),x∈R,
sin2x),x∈R,
(Ⅰ)若f(x)=1- 且x∈[-
且x∈[-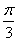 ,
, ],求x;
],求x;
(Ⅱ)若函数y=2sin2x的图象按向量 =(m,n)(|m|<
=(m,n)(|m|< )平移后得到函数y=f(x)的图象,求实数m、n的值。
)平移后得到函数y=f(x)的图象,求实数m、n的值。
 ·
· ,其中向量
,其中向量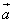 =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx, sin2x),x∈R,
sin2x),x∈R,(Ⅰ)若f(x)=1-
 且x∈[-
且x∈[-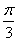 ,
, ],求x;
],求x;(Ⅱ)若函数y=2sin2x的图象按向量
 =(m,n)(|m|<
=(m,n)(|m|< )平移后得到函数y=f(x)的图象,求实数m、n的值。
)平移后得到函数y=f(x)的图象,求实数m、n的值。解:(Ⅰ)依题设,f(x)=2cos2x+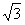 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+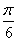 ),
),
由1+2sin(2x+ )=1-
)=1- ,得sin(2x+
,得sin(2x+ )=-
)=-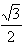 ,
,
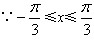 ,
,
∴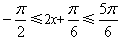 ,
,
∴2x+ ;
;
(Ⅱ)函数y=2sin2x的图象按向量 =(m,n)平移后得到函数y=2sin2(x-m)+n的图象,
=(m,n)平移后得到函数y=2sin2(x-m)+n的图象,
即函数y=f(x)的图象,
由(Ⅰ)得f(x)=2sin2(x+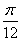 )+1,
)+1,
∵|m|<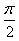 ,
,
∴m= ,n=1。
,n=1。
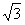 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+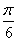 ),
),由1+2sin(2x+
 )=1-
)=1- ,得sin(2x+
,得sin(2x+ )=-
)=-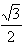 ,
,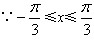 ,
,∴
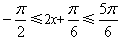 ,
,∴2x+
 ;
;(Ⅱ)函数y=2sin2x的图象按向量
 =(m,n)平移后得到函数y=2sin2(x-m)+n的图象,
=(m,n)平移后得到函数y=2sin2(x-m)+n的图象,即函数y=f(x)的图象,
由(Ⅰ)得f(x)=2sin2(x+
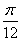 )+1,
)+1, ∵|m|<
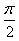 ,
,∴m=
 ,n=1。
,n=1。
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目