题目内容
在梯形ABCD中，AD∥BC，AB=5，AC=9，∠BCA=30°，∠ADB=45°，则BD等于（ ）A.9
B.
C.9
D.3
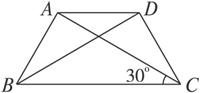
解析：如图,在△ABC中，由正弦定理得
sin∠ABC=
.
∵AD∥BC,∴∠BAD=180°-∠ABC.
∴sin∠BAD=sin∠ABC=.
在△ABD中，由正弦定理得BD=.
答案：B
练习册系列答案
黎明文化寒假作业系列答案
相关题目
黎明文化寒假作业系列答案
如图，在梯形ABCD中，AB∥CD，AD=DC=CB=a，．∠ABC=60°，平面ACFE⊥平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上．
=a，
=b，
=c，
=d，E、F分别为AB、CD的中点，则下列表达中成立的是
=
(a＋b＋c＋d)
=a，
=b，
=c，
=d，E、F分别为AB、CD的中点，则下列表达中成立的是
=
(a＋b＋c＋d)
=a，
=b，
=c,
=d,E、F分别为AB、CD的中点，则下列表达中成立的是（ ）
=
（a+b+c+d） B.
=
（c+d-a-b）
=
（a+b-c-d） D.
=
（a-b+c-d）