题目内容
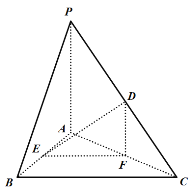
【题目】如图，在三棱锥
中，
平面ABC，点D，E，F分别为PC，AB，AC的中点．
（Ⅰ）求证：
平面DEF；
（Ⅱ）求证：
．
阅读下面给出的解答过程及思路分析．
解答：（Ⅰ）证明：在
中，因为E，F分别为AB，AC的中点，所以①．
因为
平面DEF，
平面DEF，所以平面DEF．
（Ⅱ）证明：因为平面ABC，
平面ABC，所以②．
因为D，F分别为PC，AC的中点，所以
．所以．
思路第（Ⅰ）问是先证③，再证“线面平行”；
第（Ⅱ）问是先证④，再证⑤，最后证“线线垂直”．
以上证明过程及思路分析中，设置了①~⑤五个空格，如下的表格中为每个空格给出了三个选项，其中只有一个正确，请选出你认为正确的选项，并填写在答题卡的指定位置．
空格 | 选项 | ||
① | A． | B． | C． |
② | A． | B． | C． |
③ | A．线线垂直 | B．线面垂直 | C．线线平行 |
④ | A．线线垂直 | B．线面垂直 | C．线线平行 |
⑤ | A．线面平行 | B．线线平行 | C．线面垂直 |
【答案】①A；②B；③C；④A；⑤B．
【解析】
①：由中位线分析；②线面垂直的性质分析；③由线线推导线面；④由线面垂直推导线线垂直；⑤由线线平行推导线线垂直.
①因为
是中位线，所以
，故选A；②
平面
，
平面，可通过线面垂直得到线线垂直，故选B；③通过中位线，先证线线平行，再证线面平行，故选C；④根据
可知：先证明线线垂直，故选A；⑤由
可知：再证线线平行，故选B.
练习册系列答案
相关题目
