题目内容
若函数 满足
满足 ,且
,且 时,
时, ,则函数
,则函数 的图象与函数
的图象与函数 的图象的交点的个数为 ( )
的图象的交点的个数为 ( )
A.3 B.4 C.6 D.8
【答案】
C
【解析】
试题分析:由题意知,函数 是个周期为2的周期函数,且是个偶函数,在一个周期
是个周期为2的周期函数,且是个偶函数,在一个周期 上,图象是两条斜率分别为1和-1的线段,且
上,图象是两条斜率分别为1和-1的线段,且 ,同理可得到在其他周期上的图象.函数
,同理可得到在其他周期上的图象.函数 也是个偶函数,先看在[0,+∞)上的交点个数,则它们总的交点个数是在[0,+∞)上的交点个数的2倍,在(0,+∞)上,
也是个偶函数,先看在[0,+∞)上的交点个数,则它们总的交点个数是在[0,+∞)上的交点个数的2倍,在(0,+∞)上, ,
,
图象过(1,0),和(4,1),是单调增函数,与 交与3个不同点,
交与3个不同点,
∴函数 的图象与函数
的图象与函数 的图象的交点的个数为6个,故选
的图象的交点的个数为6个,故选 .
.
考点:函数的奇偶性、周期性,对数函数的图象和性质.

练习册系列答案
相关题目







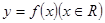 满足
满足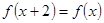 ,且
,且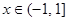 时,
时,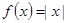 ,则函数
,则函数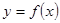 的图象与函数
的图象与函数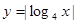 图象的交点个数为__________。
图象的交点个数为__________。 满足
满足 ,且
,且 时,
时,
 ,则函数
,则函数 在区间
在区间 内的零点的个数为
内的零点的个数为
 满足
满足 ,且
,且 时,
时, ,则函数
,则函数
 的图象的交点的个数为(
)
的图象的交点的个数为(
)