题目内容
 如图是函数y=sin(wx+φ)(w>0,|φ|<
如图是函数y=sin(wx+φ)(w>0,|φ|<| π | 2 |
分析:本题考查的知识点y=Asin(ωx+φ)中参数的物理意义,由函数图象我们易得函数的周期,进而求出ω的值,然后根据向左平移量求出φ的值.
解答:解:由图知T=
π-(-
)=π,
∴w=
=
=2,
∴y=sin(2x+φ).
又点(-
,0)在图象上,
∴sin(-
+φ)=0,
∴-
+φ=0,
∴φ=
.
| 11 |
| 12 |
| π |
| 12 |
∴w=
| 2π |
| T |
| 2π |
| π |
∴y=sin(2x+φ).
又点(-
| π |
| 12 |
∴sin(-
| π |
| 6 |
∴-
| π |
| 6 |
∴φ=
| π |
| 6 |
点评:已知函数图象求函数y=Asin(ωx+φ)(A>0,ω>0)的解析式时,常用的解题方法是待定系数法,由图中的最大值或最小值确定A,由周期确定ω,由适合解析式的点的坐标来确定φ,但由图象求得的y=Asin(ωx+φ)(A>0,ω>0)的解析式一般不唯一,只有限定φ的取值范围,才能得出唯一解,否则φ的值不确定,解析式也就不唯一.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
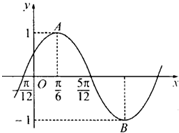 如图是函数y=sin(ωx+φ)的图象的一部分,A,B是图象上的一个最高点和一个最低点,O为坐标原点,则
如图是函数y=sin(ωx+φ)的图象的一部分,A,B是图象上的一个最高点和一个最低点,O为坐标原点,则| OA |
| OB |
A、
| ||
B、
| ||
C、
| ||
D、
|
 )的图象的一部分,则φ= ,w= .
)的图象的一部分,则φ= ,w= .
 )的图象的一部分,则φ= ,w= .
)的图象的一部分,则φ= ,w= .
 的值为( )
的值为( )



