题目内容
已知函数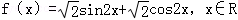
．
（I）求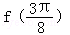
的值；
（II） 求f（x）的最大值和最小正周期；
（III） 若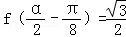
，α是第二象限的角，求sin2α．
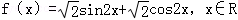．（I）求
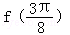的值；（II） 求f（x）的最大值和最小正周期；
（III） 若
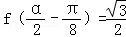，α是第二象限的角，求sin2α．解：（Ⅰ）f（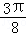
）=
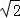sin（2×
）+
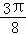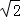cos（2×
）=
×
﹣
×
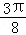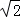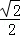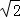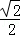=0；
（Ⅱ）∵f（x）=2（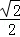
sin2x+
cos2x）=2（cos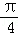
sin2x+sin
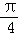cos2x）=2sin（2x+
）．
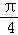∴f（x）的最大值为2，最小正周期T=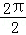
=π；
（Ⅲ）由（Ⅱ）知f（x）=2sin（2x+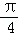
），
∴f（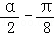
）=2sinα=
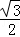，即sinα=
，
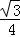又α是第二象限的角，
∴cosα=﹣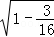
=﹣
，
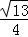∴sin2α=2sinαcosα=2×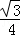
×（﹣
）=﹣
．
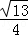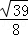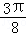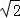）=sin（2×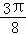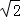）+cos（2×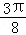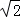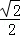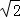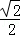）=×﹣×=0；（Ⅱ）∵f（x）=2（
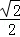sin2x+cos2x）=2（cos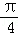sin2x+sin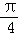cos2x）=2sin（2x+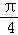）．∴f（x）的最大值为2，最小正周期T=
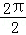=π；（Ⅲ）由（Ⅱ）知f（x）=2sin（2x+
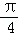），∴f（
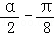）=2sinα=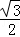，即sinα=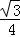，又α是第二象限的角，
∴cosα=﹣
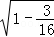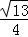=﹣，∴sin2α=2sinαcosα=2×
×（﹣）=﹣．
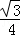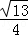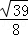练习册系列答案
相关题目
．
的值；
，
的单调区间；
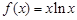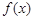上的最小值。
。
的最小值；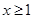
都有
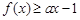，求实数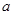
的取值范围。
，
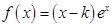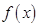的单调区间；（II）求
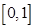上的最小值。
。
的单调区间；
成立，求实数
的取值范围。