题目内容
4.已知C${\;}_{2}^{2}$+C${\;}_{3}^{2}$+…+C${\;}_{n}^{2}$=C${\;}_{8}^{3}$(n∈N*).(1)求n的值;
(2)求二项式($\sqrt{x}$-$\frac{2}{\root{3}{x}}$)n展开式的一次项.
分析 (1)由条件利用二项式系数的性质,求得 ${C}_{n+1}^{3}$=C${\;}_{8}^{3}$,由此可得n的值.
(2)由条件利用二项展开式的通项公式,求得展开式的一次项.
解答 解:(1)∵C${\;}_{2}^{2}$+C${\;}_{3}^{2}$+…+C${\;}_{n}^{2}$=C${\;}_{8}^{3}$=${C}_{3}^{3}$+C${\;}_{3}^{2}$+…+C${\;}_{n}^{2}$=${C}_{n+1}^{3}$=C${\;}_{8}^{3}$,∴n=7.
(2)二项式($\sqrt{x}$-$\frac{2}{\root{3}{x}}$)n =($\sqrt{x}$-$\frac{2}{\root{3}{x}}$)7 的展开式的通项公式为Tr+1=${C}_{7}^{r}$•(-2)r•${x}^{\frac{7}{2}-\frac{5r}{6}}$,
令$\frac{7}{2}$-$\frac{5r}{6}$=1,求得r=3,可得展开式的一次项为 T4=${C}_{7}^{3}$•(-2)3•x=-280x.
点评 本题主要考查二项式系数的性质,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
相关题目
14.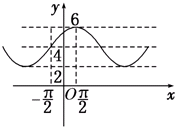 已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
 已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )| A. | y=2cos($\frac{x}{2}$-$\frac{π}{4}$)+4 | B. | y=2cos($\frac{x}{2}$+$\frac{π}{4}$)+4 | C. | y=4cos($\frac{x}{2}$-$\frac{π}{4}$)+2 | D. | y=4cos($\frac{x}{2}$+$\frac{π}{4}$)+2 |
12.在△ABC中,已知M是BC中点,设$\overrightarrow{CB}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$,则$\overrightarrow{AM}$=( )
| A. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | C. | $\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | D. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ |
9.已知sinα=-$\frac{1}{3}$,且α∈(-$\frac{π}{2}$,$\frac{π}{2}}$),则tanα=( )
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $-\frac{{\sqrt{2}}}{4}$ | C. | $±\frac{{\sqrt{2}}}{4}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
14.现有历史、政治、数学、物理、化学共有5本书,从中任取2本,取出的书至少有一本文科书的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |