题目内容
求直线y=x+
思路解析:可以求出交点坐标,再利用两点间的距离公式求解;也可以利用弦长公式. 解法一:先求交点A、B,如图 解方程组y=x+ 得x2-2x-3=0. 解得 直线被曲线截得的线段长|AB|= 解法二:设交点的坐标A(x1,y1)、B(x2,y2),则y1=x1+ ∴y1-y2=x1-x2.由 ∴x1+x2=2,x1x2=-3. 弦长:|AB|= = 深化升华 解法二中设出了交点坐标,但未求交点坐标,这是应用了“设而不求”的解题技巧,要注意掌握. 一般地,设直线l的方程:y=kx+b,曲线C的方程:F(x,y)=0, 直线l与曲线C的交点为A(x1,y1)、B(x2,y2). 则y1=kx1+b,y2=kx2+b,∴y1-y2=k(x1-x2). 由 ∴|AB|= = 这个式子就是求弦长公式,以后在解圆锥曲线有关问题时要经常用到.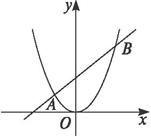
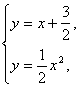 消去y,
消去y,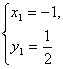 或
或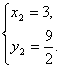 ∴A(-1,
∴A(-1,![]() )、B(3,
)、B(3,![]() ).
).![]() =4
=4![]() .
.![]() ,y2=x2+
,y2=x2+![]() .
.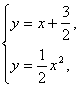 消去y,得x2-2x-3=0.
消去y,得x2-2x-3=0.![]() =
=![]()
![]() ·
·![]() =
=![]() ·
·![]() =4
=4![]() .
.![]() 消去y,得ax2+mx+c=0.∴x1+x2=-
消去y,得ax2+mx+c=0.∴x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.![]() =
=![]()
![]() =
=![]() ·
·![]() .
.

灿烂在六月模拟强化测试精编系列答案
测试卷全新升级版系列答案
测试新方案系列答案
常德标准卷系列答案
超级奥赛培优竞赛系列答案
超级考卷系列答案
超级培优系列答案
超级英语系列答案
晨光全优同步指导训练与检测系列答案
成功宝典系列答案
 (2012•杨浦区二模)如图,椭圆C1:
(2012•杨浦区二模)如图,椭圆C1: