题目内容
(本题满分14分)已知函数 .
.
(1)求函数 的定义域;
的定义域;
(2)判断 的奇偶性;
的奇偶性;
(3)方程 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使

 ;如果没有,请说明理由?(注:区间的长度为
;如果没有,请说明理由?(注:区间的长度为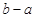 ).
).
 .
.(1)求函数
 的定义域;
的定义域;(2)判断
 的奇偶性;
的奇偶性;(3)方程
 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使

 ;如果没有,请说明理由?(注:区间的长度为
;如果没有,请说明理由?(注:区间的长度为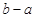 ).
).解:(1),由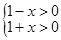 得
得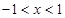 故函数
故函数 的定义域为
的定义域为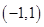 …2分
…2分
(2)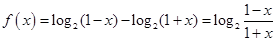
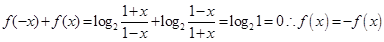 ,故
,故 为奇函
为奇函
数.…………6分
 (3)方程
(3)方程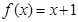 可化为
可化为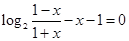 ,令
,令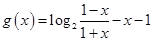
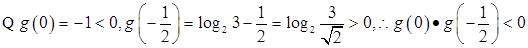
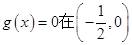 内有根.即方程
内有根.即方程 有根
有根 ,
, 
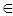
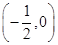 ……10分
……10分
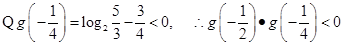 , 有
, 有

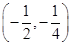 ,此时
,此时
区间长度为
综上方程 有根
有根 ,使
,使

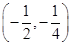 ,
,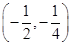 即为所求长度为的
即为所求长度为的 区
区
间…….…………14分
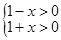 得
得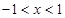 故函数
故函数 的定义域为
的定义域为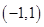 …2分
…2分(2)
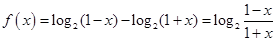
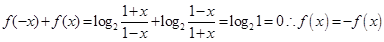 ,故
,故 为奇函
为奇函数.…………6分
 (3)方程
(3)方程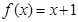 可化为
可化为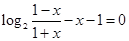 ,令
,令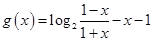
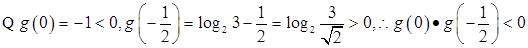
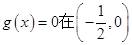 内有根.即方程
内有根.即方程 有根
有根 ,
, 
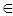
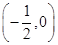 ……10分
……10分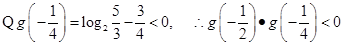 , 有
, 有

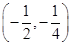 ,此时
,此时区间长度为

综上方程
 有根
有根 ,使
,使

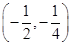 ,
,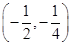 即为所求长度为的
即为所求长度为的 区
区间…….…………14分
略

练习册系列答案
相关题目
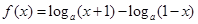 ,
,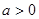 且
且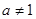 .
.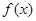 的定义域;(Ⅱ)判断
的定义域;(Ⅱ)判断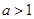 时,求使
时,求使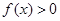 的
的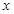 的取值范围.
的取值范围. 为奇函数,
为奇函数, 为常数.
为常数. 在区间(1,+∞)的单调性,并说明理由;
在区间(1,+∞)的单调性,并说明理由; 值,不等式
值,不等式 恒成立,求实数
恒成立,求实数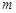 的取值范围.
的取值范围.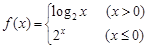 ,若
,若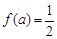 ,则实数
,则实数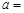 ( )
( )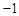
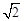
 或
或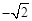
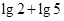 = .
= . 等于( )
等于( )



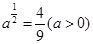 ,则
,则 ▲ .
▲ . ,
, ,则
,则 (用
(用 表示)
表示)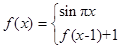 ,则
,则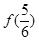 的值为 ※ .
的值为 ※ .