题目内容
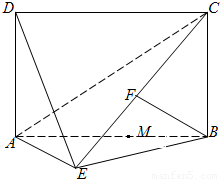
.如图,四边形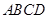 为矩形,
为矩形,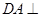 平面
平面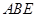 ,
,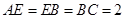 ,
,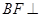 平面
平面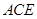 于点
于点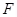 ,且点
,且点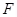 在
在 上.
上.
(1)求证: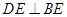 ;(2)求四棱锥
;(2)求四棱锥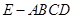 的体积;
的体积;
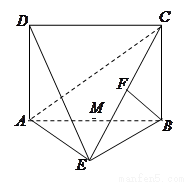
(3)设点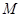 在线段
在线段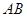 上,且
上,且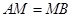 ,试在线段
,试在线段 上确定一点
上确定一点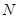 ,使得
,使得 平面
平面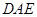 .
.
【答案】
(1)见解析;
(2)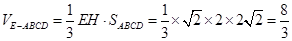 ;
;
(3)点 就是点
就是点 。
。
【解析】本试题主要是考查了线线垂直的证明以及棱锥的体积公式,以及线面平行的证明的综合运用。
(1)要证明线线垂直,先利用线面垂直的性质定理得到结论。
(2)利用转换顶点的思想求解三棱锥的体积的运算。
(3)根据线面平行的判定定理得到证明,关键是线线平行的证明.
解:(1)因为 平面
平面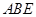 ,
,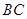 ∥
∥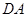 ,所以
,所以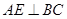 ,
,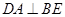
因为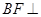 平面
平面 于点
于点 ,
,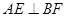 …………………………………3分
…………………………………3分
因为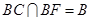 ,所以
,所以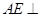 面
面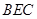 ,则
,则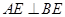
因为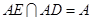 ,所以
,所以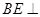 面
面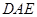 ,则
,则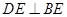 ………………………5分
………………………5分
(2)作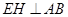 ,因为面
,因为面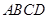
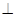 平面
平面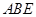 ,所以
,所以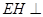 面
面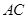
因为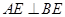 ,
,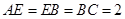 ,所以
,所以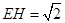 …………………………7分
…………………………7分

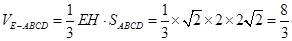 …………………………………9分
…………………………………9分
(3)因为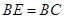 ,
,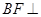 平面
平面 于点
于点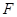 ,所以
,所以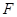 是
是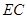 的中点
的中点
设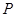 是
是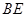 的中点,连接
的中点,连接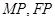 …………………………12分
…………………………12分
所以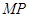 ∥
∥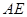
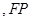 ∥
∥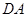
因为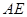
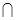
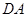
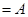 ,所以
,所以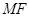 ∥面
∥面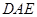 ,则点
,则点 就是点
就是点 …14分
…14分

练习册系列答案
相关题目
 为矩形,
为矩形, 平面
平面 ,
, 为
为 上的点,且
上的点,且 平面
平面 .
. 
 的体积;
的体积; 在线段
在线段 上,且满足
上,且满足 ,试在线段
,试在线段 ,使得
,使得 平面
平面 .
. 为矩形,平面
为矩形,平面 ,
,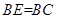 ,
, 为
为 上的一点,且
上的一点,且 ⊥平面
⊥平面 .
.

 ⊥
⊥ ;
; .
. 为矩形,且
为矩形,且 ,
, ,
, 为
为 上的动点。
上的动点。
 ;
; ,在线段
,在线段 上存在这样的点E,使得二面角
上存在这样的点E,使得二面角 的平面角大小为
的平面角大小为 。试确定点E的位置。
。试确定点E的位置。 为矩形,
为矩形,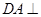 平面
平面 ,
, ,
, 平面
平面 于点
于点 ,且点
,且点 上,点
上,点 是线段
是线段 的中点。
的中点。 ;
; 的体积;
的体积; ,使得
,使得 平面
平面 。
。
 为矩形,
为矩形, ,
, ,以
,以 为圆心,1为半径作四分之一个圆弧
为圆心,1为半径作四分之一个圆弧 ,在圆弧
,在圆弧 ,则直线
,则直线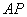 与线段
与线段 有公共点的概率是
有公共点的概率是 