题目内容
设椭圆C:
+
=1的左焦点为F,左准线为l,一条直线过点F与椭圆C交于A,B两点,若直线l上存在点P,使△ABP为等边三角形,求直线AB的方程.
| x2 |
| 4 |
| y2 |
| 2 |
分析:设过点F的弦AB的中点为M,分别过A,B,M向准线l作垂线,垂足分别为A1,B1,M1,则|MM1|=
(|AA1|+|BB1|)=
(
+
)=
|AB|,又因为△PAB为等边三角形?|PM|=
|AB|,所以
=
,cos∠PMM1=
,由此能求出AB的方程.
| 1 |
| 2 |
| 1 |
| 2 |
| |AF| |
| e |
| |BF| |
| e |
| 1 | ||
|
| ||
| 2 |
| |MM1| |
| |MP| |
| ||
| 3 |
| ||
| 3 |
解答:解:如图,∵F(-
,0),l:x=-2
,离心率e=
.设过点F的弦AB的中点为M,分别过A,B,M向准线l作垂线,垂足分别为A1,B1,M1,则|MM1|=
(|AA1|+|BB1|)=
(
+
)=
|AB|,又因为△PAB为等边三角形?|PM|=
|AB|,所以
=
,
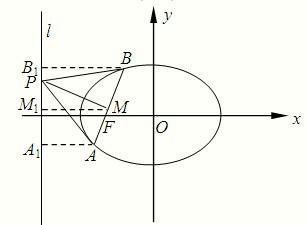
即cos∠PMM1=
,
∴sin∠PMM1=
,tam∠PMM1=
,
又kPM=±tam∠PMM1=±
∵AB⊥PM,∴kAB=-
=±
,
又AB过点F(-
,0),所以AB的方程为y=±
(x+
).
即直线AB的方程为:
x-y+2=0,或
x+y+2=0.
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| |AF| |
| e |
| |BF| |
| e |
| 1 | ||
|
| ||
| 2 |
| |MM1| |
| |MP| |
| ||
| 3 |

即cos∠PMM1=
| ||
| 3 |
∴sin∠PMM1=
| ||
| 3 |
| ||
| 2 |
又kPM=±tam∠PMM1=±
| ||
| 2 |
∵AB⊥PM,∴kAB=-
| 1 |
| kPM |
| 2 |
又AB过点F(-
| 2 |
| 2 |
| 2 |
即直线AB的方程为:
| 2 |
| 2 |
点评:本题考查圆锥曲线的基本几何量的求法,如焦点、准线、离心率等.考查直线与圆锥曲线的基本问题的研究方法,如弦长计算、弦中点坐标求法等.考查圆锥曲线的定义的灵活应用.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
 在平面直角坐标系xOy中,如图,已知椭圆C:
在平面直角坐标系xOy中,如图,已知椭圆C: (2012•江苏二模)如图,已知椭圆C:
(2012•江苏二模)如图,已知椭圆C: