题目内容
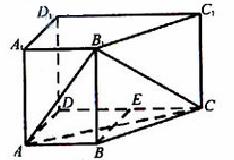
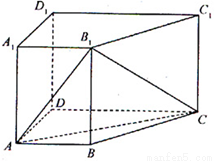
如图,在四棱柱![]() 中,侧面
中,侧面![]() ⊥底面
⊥底面![]() ,
,![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]()
![]() ,O为
,O为![]() 中点。
中点。
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求锐二面角A—C1D1—C的余弦值。
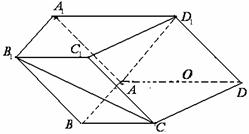
(Ⅰ)证明:如图,连接![]() , …………..1分
, …………..1分
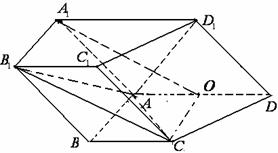
则四边形![]() 为正方形, …………..2分
为正方形, …………..2分
![]() ,且
,且![]()
故四边形![]() 为平行四边形,…………..3分
为平行四边形,…………..3分
![]() , …………..4分
, …………..4分
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ……..5分
……..5分
![]() 平面
平面![]() …………..6分
…………..6分
(Ⅱ)![]() 为
为![]() 的中点,
的中点,![]() ,又侧面
,又侧面![]() ⊥底面
⊥底面![]() ,故
,故![]() ⊥底面
⊥底面![]() ,…………..7分
,…………..7分
以![]() 为原点,所
为原点,所![]() 在直线分别为
在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的坐标系,
轴建立如图所示的坐标系,

则![]()
![]() ,…………..8分
,…………..8分
![]()
![]() ,…………..9分
,…………..9分
设![]() 为平面
为平面![]() 的一个法向量,由
的一个法向量,由![]() ,得
,得![]() ,
,
令![]() ,则
,则![]() ………..10分
………..10分
又设![]() 为平面
为平面![]() 的一个法向量,由
的一个法向量,由![]() ,得
,得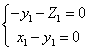 ,令
,令
![]() ,则
,则![]() ,………..11分
,………..11分
则![]() ,故所求锐二面角A—C1D1—C的余弦值为
,故所求锐二面角A—C1D1—C的余弦值为![]() ………..12分
………..12分
注:第2问用几何法做的酌情给分。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,侧棱
中,侧棱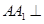 底面
底面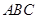 ,
,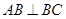 ,
,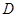 为
为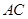 的中点,
的中点,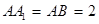 .
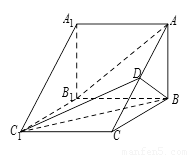
.
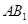 //平面
//平面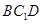 ;
;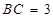 ,求四棱锥
,求四棱锥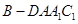 的体积.
的体积. 中,侧棱
中,侧棱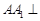 底面
底面 ,
,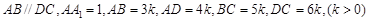
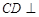 平面
平面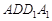
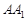 与平面
与平面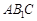 所成角的正弦值为
所成角的正弦值为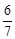 ,求
,求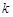 的值
的值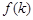 ,写出
,写出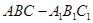 中,侧棱
中,侧棱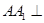 底面
底面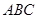 ,
,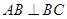 ,
,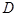 为
为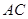 的中点,
的中点,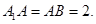
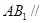 平面
平面 ;
;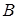 作
作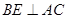 于点
于点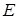 ,求证:直线
,求证:直线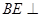 平面
平面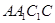
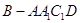 的体积为3,求
的体积为3,求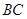 的长度
的长度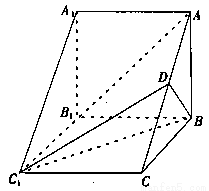
 中,底面
中,底面 是正方形,侧棱与底面垂直,
是正方形,侧棱与底面垂直, 分别是
分别是 ,
, 的中点,则以下结论中不成立的是( )
的中点,则以下结论中不成立的是( )
 与
与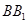 垂直
B.
垂直
B. 垂直
垂直  异面
D.
异面
D. 异面
异面