题目内容
已知各项为正数的等比数列{an}(n∈N*)的公比为q(q≠1),有如下真命题:若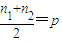 ,则
,则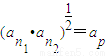 (其中n1、n2、p为正整数).
(其中n1、n2、p为正整数).(1)若
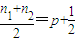 ,试探究
,试探究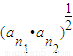 与ap、q之间有何等量关系,并给予证明;
与ap、q之间有何等量关系,并给予证明;(2)对(1)中探究得出的结论进行推广,写出一个真命题,并给予证明.
【答案】分析:(1)根据若 可知n1+n2=2p+1,再根据an的通项公式代入
可知n1+n2=2p+1,再根据an的通项公式代入 中,进而可得
中,进而可得 ,答案可得.
,答案可得.
(2)若 是公比为q的等比数列{an}的任意m项,
是公比为q的等比数列{an}的任意m项,
假设 时,再由(1)中结论可推断可得一真命题;
时,再由(1)中结论可推断可得一真命题;
假设 互素)时,同样可得一真命题.
互素)时,同样可得一真命题.
解答:解:(1)因为 ,所以n1+n2=2p+1,又an=a1qn-1
,所以n1+n2=2p+1,又an=a1qn-1
即
(2)若 是公比为q的等比数列{an}的任意m项,则存在以下真命题:
是公比为q的等比数列{an}的任意m项,则存在以下真命题:
①若 ,则有
,则有 成立.
成立.
②若 互素),则有
互素),则有 成立.
成立.
点评:本题主要考查了等比数列的性质.考查学生根据已知结论分析问题和解决问题的能力.
 可知n1+n2=2p+1,再根据an的通项公式代入
可知n1+n2=2p+1,再根据an的通项公式代入 中,进而可得
中,进而可得 ,答案可得.
,答案可得.(2)若
 是公比为q的等比数列{an}的任意m项,
是公比为q的等比数列{an}的任意m项,假设
 时,再由(1)中结论可推断可得一真命题;
时,再由(1)中结论可推断可得一真命题;假设
 互素)时,同样可得一真命题.
互素)时,同样可得一真命题.解答:解:(1)因为
 ,所以n1+n2=2p+1,又an=a1qn-1
,所以n1+n2=2p+1,又an=a1qn-1
即

(2)若
 是公比为q的等比数列{an}的任意m项,则存在以下真命题:
是公比为q的等比数列{an}的任意m项,则存在以下真命题:①若
 ,则有
,则有 成立.
成立.②若
 互素),则有
互素),则有 成立.
成立.点评:本题主要考查了等比数列的性质.考查学生根据已知结论分析问题和解决问题的能力.

练习册系列答案
相关题目