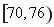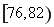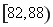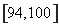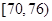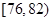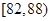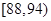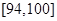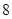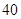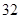题目内容
生产A，B两种元件，其质量按测试指标划分为：指标大于或等于
为正品，小于为次品．现随机抽取这两种元件各
件进行检测，检测结果统计如下：
| 测试指标 |
|
|
|
|
|
| 元件A |
|
|
|
|
|
| 元件B |
|
|
|
|
|
（Ⅰ）试分别估计元件A，元件B为正品的概率；
（Ⅱ）生产一件元件A，若是正品可盈利40元，若是次品则亏损5元；生产一件元件B，若是正品可盈利50元，若是次品则亏损10元.在（Ⅰ）的前提下，
（ⅰ）记
为生产1件元件A和1件元件B所得的总利润，求随机变量的分布列和数学期望；
（ⅱ）求生产5件元件B所获得的利润不少于140元的概率．
解：（Ⅰ）解：元件A为正品的概率约为
． …………1分
元件B为正品的概率约为
． ………………2分
（Ⅱ）解：（ⅰ）随机变量的所有取值为
． ………………3分
； 
；
； 
． ………………7分
所以，随机变量的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
． ………8分
（ⅱ）设生产的5件元件B中正品有
件，则次品有
件.
依题意，得 
， 解得 
．
所以 
，或
．…10分
设“生产5件元件B所获得的利润不少于140元”为事件
，
则 
． ………………12分
一诺书业暑假作业快乐假期云南美术出版社系列答案生产A，B两种元件，其质量按测试指标划分为：指标大于或等于82为正品，小于82为
次品，现随机抽取这两种元件各100件进行检测，检测结果统计如下：
测试指标 |
|
|
|
|
|
元件A | 8 | 12 | 40 | 32 | 8 |
元件B | 7 | 18 | 40 | 29 | 6 |
（Ⅰ）试分别估计元件A、元件B为正品的概率；
（Ⅱ）生产一件元件A，若是正品可盈利50元，若是次品则亏损10元；生产一件元件B，若是正品可盈利100元，若是次品则亏损20元，在（Ⅰ）的前提下；
（i）求生产5件元件B所获得的利润不少于300元的概率；
（ii）记X为生产1件元件A和1件元件B所得的总利润，求随机变量X的分布列和数学期望．
生产A，B两种元件，其质量按测试指标划分为：指标大于或等于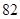
为正品，小于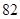为次品．现随机抽取这两种元件各
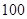件进行检测，检测结果统计如下：
|
测试指标 |
|
|
|
|
|
|
元件A |
|
|
|
|
|
|
元件B |
|
|
|
|
|
（Ⅰ）试分别估计元件A，元件B为正品的概率；
（Ⅱ）生产一件元件A，若是正品可盈利40元，若是次品则亏损5元；生产一件元件B，若是正品可盈利50元，若是次品则亏损10元.在（Ⅰ）的前提下，
（ⅰ）记
为生产1件元件A和1件元件B所得的总利润，求随机变量的分布列和数学期望；
（ⅱ）求生产5件元件B所获得的利润不少于140元的概率．