题目内容
已知向量 ,
,
 ________.
________.
120°
分析:由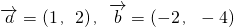 知,此两向量共线,又
知,此两向量共线,又 =-
=- ,故
,故 与
与 的夹角为
的夹角为 与
与 的夹角的补角,故求出
的夹角的补角,故求出 与
与 的夹角即可,由题设条件
的夹角即可,由题设条件 利用向量的夹角公式易求得
利用向量的夹角公式易求得 与
与 的夹角
的夹角
解答:由题意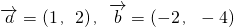 ,故有
,故有 =(-1,-2)=-
=(-1,-2)=- ,故
,故 与
与 的夹角为
的夹角为 与
与 的夹角的补角,令
的夹角的补角,令 与
与 的夹角为θ
的夹角为θ
又 ,
,
∴cosθ= =
= ,
,
∴θ=60°
故 与
与 的夹角为120°
的夹角为120°
故答案为:120°
点评:本题考查数量积表示两个向量的夹角,解题的关键是熟练掌握两个向量夹角公式,本题有一易错点,易因为没有理解清楚 与
与 的夹角为
的夹角为 与
与 的夹角的补角导致求解失败
的夹角的补角导致求解失败
分析:由
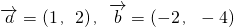 知,此两向量共线,又
知,此两向量共线,又 =-
=- ,故
,故 与
与 的夹角为
的夹角为 与
与 的夹角的补角,故求出
的夹角的补角,故求出 与
与 的夹角即可,由题设条件
的夹角即可,由题设条件 利用向量的夹角公式易求得
利用向量的夹角公式易求得 与
与 的夹角
的夹角解答:由题意
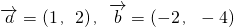 ,故有
,故有 =(-1,-2)=-
=(-1,-2)=- ,故
,故 与
与 的夹角为
的夹角为 与
与 的夹角的补角,令
的夹角的补角,令 与
与 的夹角为θ
的夹角为θ又
 ,
,
∴cosθ=
 =
= ,
,∴θ=60°
故
 与
与 的夹角为120°
的夹角为120°故答案为:120°
点评:本题考查数量积表示两个向量的夹角,解题的关键是熟练掌握两个向量夹角公式,本题有一易错点,易因为没有理解清楚
 与
与 的夹角为
的夹角为 与
与 的夹角的补角导致求解失败
的夹角的补角导致求解失败 
练习册系列答案
相关题目