题目内容
已知函数f(x)=log3(ax+b)的图象经过点A(2,1)和B(5,2),记an=3f(n),n∈N*。
(1)求数列{an}的通项公式;
(2)设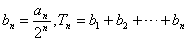 ,若Tn<m(m∈Z),求m的最小值;
,若Tn<m(m∈Z),求m的最小值;
(3)求使不等式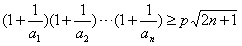 对一切n∈N*均成立的最大实数p。
对一切n∈N*均成立的最大实数p。
(1)求数列{an}的通项公式;
(2)设
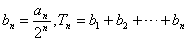 ,若Tn<m(m∈Z),求m的最小值;
,若Tn<m(m∈Z),求m的最小值;(3)求使不等式
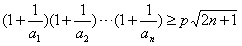 对一切n∈N*均成立的最大实数p。
对一切n∈N*均成立的最大实数p。 解:(1)由题意,得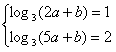 ,解得:
,解得: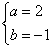 ,
,
∴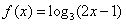 ,
,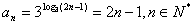 。
。
(2)由(1)得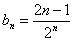 ,
,
∴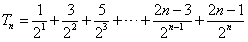 , ①
, ①
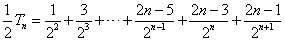 , ②
, ②
①-②得,
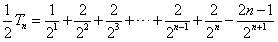
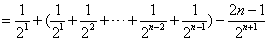
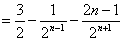 ,
,
∴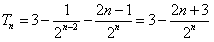 ,
,
设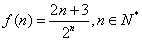 ,
,
则由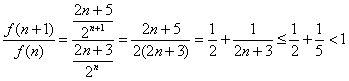 ,
,
得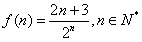 随n的增大而减小,
随n的增大而减小,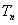 随n的增大而增大,
随n的增大而增大,
∴当n→+∞时,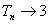 ,
,
又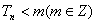 恒成立,
恒成立,
∴mmin=3。
(3)由题意得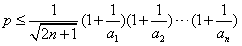 对n∈N*恒成立,
对n∈N*恒成立,
记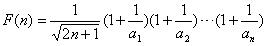 ,
,
则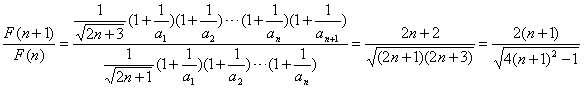 ,
,
∵F(n)>0,
∴F(n+1)>F(n),即F(n)是随n的增大而增大,
∴F(n)的最小值为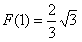 ,
,
∴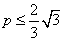 ,即
,即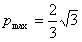 。
。
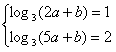 ,解得:
,解得: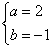 ,
,∴
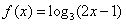 ,
,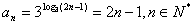 。
。(2)由(1)得
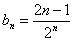 ,
,∴
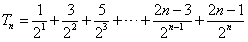 , ①
, ① 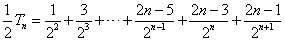 , ②
, ② ①-②得,
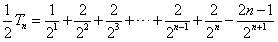
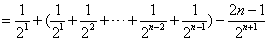
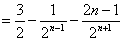 ,
,∴
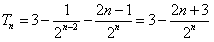 ,
, 设
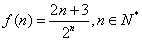 ,
,则由
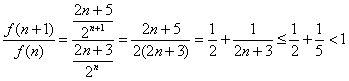 ,
,得
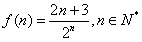 随n的增大而减小,
随n的增大而减小,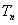 随n的增大而增大,
随n的增大而增大,∴当n→+∞时,
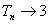 ,
,又
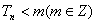 恒成立,
恒成立,∴mmin=3。
(3)由题意得
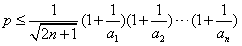 对n∈N*恒成立,
对n∈N*恒成立,记
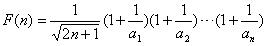 ,
,则
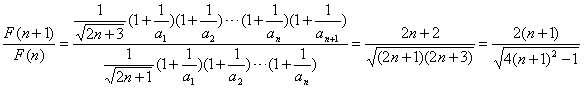 ,
,∵F(n)>0,
∴F(n+1)>F(n),即F(n)是随n的增大而增大,
∴F(n)的最小值为
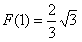 ,
,∴
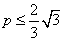 ,即
,即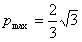 。
。
练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目