Question

椭圆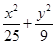=1上一点M到左焦点F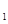的距离为2, N是MF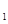的中点,则=(  )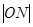

A．2                B．4                C．6                D．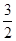

 

Answer 1

【答案】

B

【解析】

试题分析：解：∵椭圆方程为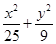,∴椭圆的a=5，长轴2a=10，可得椭圆上任意一点到两个焦点F₁、F₂距离之和等于10．

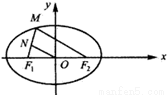
∴|MF₁|+|MF₂|=10，∵点M到左焦点F₁的距离为2，即|MF₁|=2，∴|MF₂|=10-2=8，∵△MF₁F₂中，N、O分别是MF₁、F₁F₂中点，∴|ON|=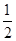 |MF₂|=4．故选B．

考点：三角形中位线定理和椭圆的定义

点评：本题考查了三角形中位线定理和椭圆的定义等知识点，考查学生的计算能力，属于基础题