题目内容
我们知道平面上n条直线最多可将平面分成1+
个部分,则空间内n个平面最多可将空间分成
(n3+5n+6)
(n3+5n+6)个部分.
| n(n+1) |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
分析:根据平面中的几何元素与空间中几何元素的对应关系:线对应面、面对应体,理解空间是怎么被分割的,找到关系式,再类比数列中的累加法即可得解
解答:解:假设n个平面可把空间分成f(n)部分,再加上第n+1个平面后可把空间分成f(n+1)部分,
∵第n+1个平面与前n个平面都相交,
∴第n+1个平面内有n交线,且这n条直线最多可把第n+1个平面分成1+
部分,
又∵平面的每一部分可把它原来所在的空间分成2部分,
∴f(n+1)=f(n)+1+
,
∴f(n+1)-f(n)=1+
=1+
+
,
∴f(2)-f(1)=1+
+
,
f(3)-f(2)=1+
+
,
…
f(n)-f(n-1)=1+
+
,
上式相加得:f(n)-f(1)=(n-1)+
×
+
×
=
-1,
∴f(n)=
+1=
(n3+5n+6)
故答案为:
(n3+5n+6)
∵第n+1个平面与前n个平面都相交,
∴第n+1个平面内有n交线,且这n条直线最多可把第n+1个平面分成1+
| n(n+1) |
| 2 |
又∵平面的每一部分可把它原来所在的空间分成2部分,
∴f(n+1)=f(n)+1+
| n(n+1) |
| 2 |
∴f(n+1)-f(n)=1+
| n(n+1) |
| 2 |
| n2 |
| 2 |
| n |
| 2 |
∴f(2)-f(1)=1+
| 12 |
| 2 |
| 1 |
| 2 |
f(3)-f(2)=1+
| 22 |
| 2 |
| 2 |
| 2 |
…
f(n)-f(n-1)=1+
| (n-1)2 |
| 2 |
| n-1 |
| 2 |
上式相加得:f(n)-f(1)=(n-1)+
| 1 |
| 2 |
| (n-1)n(2n-1) |
| 6 |
| 1 |
| 2 |
| (n-1)n |
| 2 |
| n3+5n |
| 6 |
∴f(n)=
| n3+5n |
| 6 |
| 1 |
| 6 |
故答案为:
| 1 |
| 6 |
点评:本题考察归纳推理,需要有比较好的抽象思维,同时考察累加法的应用.属难题

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
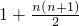 个部分,则空间内n个平面最多可将空间分成________个部分.
个部分,则空间内n个平面最多可将空间分成________个部分. 个部分,则空间内n个平面最多可将空间分成 个部分.
个部分,则空间内n个平面最多可将空间分成 个部分. 段,平面上n条直线最多将平面分成
段,平面上n条直线最多将平面分成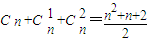 部分(规定:若k>n则
部分(规定:若k>n则 =0),则类似地可以推算得到空间里n个平面最多将空间分成 部分.
=0),则类似地可以推算得到空间里n个平面最多将空间分成 部分.