Question

已知椭圆C₁：

x2

3

+

y2

2

=1的左焦点为F₁，右焦点为F₂．
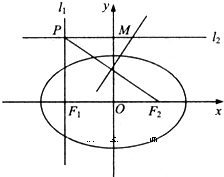
（Ⅰ）设直线l₁过点F₁且垂直于椭圆的长轴，动直线l₂垂直l₁于点P，线段PF₂的垂直平分线交l₂于点M，求点M的轨迹C₂的方程；
（Ⅱ）设O为坐标原点，取曲线C₂上不同于O的点S，以OS为直径作圆与C₂相交另外一点R，求该圆的面积最小时点S的坐标．

Answer 1

分析：（I）利用椭圆的方程即可得出c及直线l₁的方程，再利用抛物线的定义即可得出点M的轨迹C₂的方程；
（II）由于以OS为直径的圆与C₂相交于点R，可得∠ORS=90°，设S（x₁，y₁），R（x₂，y₂），则

y

2 1

=4x1，

y

2 2

=4x2，利用

OR

•

SR

=x₂（x₂-x₁）+y₂（y₂-y₁）=0，和基本不等式可得|y₁|_min及|x₁|_min，进而得到圆的直径的最小值|OS|_min即可．

解答：解：（I）由椭圆方程

x2

3

+

y2

2

=1，可得a²=3，b²=2，∴c=

a2-b2

=1．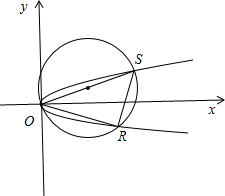
∴直线l₁：x=-1，焦点F₂（1，0）．
∵点M在线段PF₂的垂直平分线上，∴|MP|=|MF₂|，
故动点M到定直线l₁：x=-1的距离等于它到定点F₂（1，0）的距离，
因此动点M的轨迹C₂是以l₁为准线，F₂为焦点的抛物线，
所以点M的轨迹C₂的方程为y²=4x
（II）∵以OS为直径的圆与C₂相交于点R，
∴∠ORS=90°，即

OR

•

SR

=0．
设S（x₁，y₁），R（x₂，y₂），则

y

2 1

=4x1，

y

2 2

=4x2，

SR

=(x2-x1，y2-y1)，

OR

=(x2，y2)．
∴

OR

•

SR

=x₂（x₂-x₁）+y₂（y₂-y₁）=0，即

y 2 2 ( y 2 2 - y 2 1 )

16

+y₂（y₂-y₁）=0．
∵y₁≠y₂，y₂≠0，∴y1=-(y2+

16

y2

)
故|y1|=|y2|+

16

|y2|

≥8，当且仅当y₂=±4时等号成立
当|y₁|_min=8时，(x1)min=

82

4

=16，圆的直径|OS|min=

162+82

=8

5

，
这时点S的坐标为（16，±8）．

点评：熟练掌握椭圆、抛物线及圆的定义及其性质、∠ORS=90°?

OR

•

SR

=0、基本不等式的性质、勾股定理等是解题的关键．