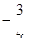题目内容
已知双曲线 的左右焦点分别为
的左右焦点分别为 ,其一条渐近线方程为
,其一条渐近线方程为 ,点
,点 在该双曲线上,则
在该双曲线上,则 = ( )
= ( )
A. | B. | C.0 | D.4 |
C
解析考点:双曲线的简单性质.
分析:由题设知b=  ,再根据点
,再根据点 在该双曲线上知y
在该双曲线上知y =1.由此能求出
=1.由此能求出  ?
?  .
.
解答:解:∵双曲线 的渐近线方程为y=±
的渐近线方程为y=± bx=±x,
bx=±x,
∴b= .
.
把点 代入双曲线,得
代入双曲线,得 -
- =1,解得y
=1,解得y =1.
=1.
∴P( ,1),F
,1),F (-2,0),F
(-2,0),F (2,0),
(2,0), ?
?  .=(-2-
.=(-2- ,0-1)?(2-
,0-1)?(2- ,0-1)=0,
,0-1)=0,
或P( ,-1),F
,-1),F (-2,0),F
(-2,0),F (2,0),
(2,0), ?
?  =(-2-
=(-2- ,0+1)?(2-
,0+1)?(2- ,0+1)=0.
,0+1)=0.
故答案为0.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
给出下列曲线:
① 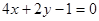 ;②
;② 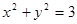 ;③
;③  ;④
;④ 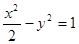 .
.
其中与直线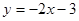 有公共点的所有曲线是 ( )
有公共点的所有曲线是 ( )
| A.①③ | B.②④ | C.①②③ | D.②③④ |
设点P(x,y)(xy≠0)是曲线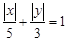 上的点,下列关系正确的是( )
上的点,下列关系正确的是( )
A. | B. |
C. | D.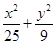 的值与1的大小关系不确定 的值与1的大小关系不确定 |
方程 表示焦点在y轴上的椭圆,则k的取值范围是 ( )
表示焦点在y轴上的椭圆,则k的取值范围是 ( )
A.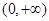 | B.(0,2) | C.(1,+∞) | D.(0,1) |
以椭圆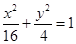 内的点
内的点 为中点的弦所在直线方程 ( )
为中点的弦所在直线方程 ( )
A.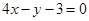 | B. | C.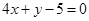 | D.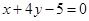 |
直线 经过椭圆
经过椭圆 的一个焦点和一个顶点,则该椭圆的离心率为. ( )
的一个焦点和一个顶点,则该椭圆的离心率为. ( )
A. | B. | C. | D. |
 ( )
( )
| A.(1,1) | B.(1,2) | C.(2,2) | D.(2,4) |
x= 表示的曲线是 ( )
表示的曲线是 ( )
| A.双曲线 | B.椭圆 | C.双曲线的一部分 | D.椭圆的一部分 |
 的顶点,过点D(0,4)的直线
的顶点,过点D(0,4)的直线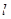 交抛物线
交抛物线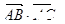 等于( )
等于( )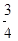 B.0 C.-3 D.
B.0 C.-3 D.