题目内容
若函数f(x)在定义域D内某区间I上是增函数,而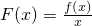 在I上是减函数,则称函数y=f(x)在I上是“慢增函数”.若函数h(x)=x2
在I上是减函数,则称函数y=f(x)在I上是“慢增函数”.若函数h(x)=x2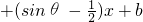 (θ,b是常数)在(0,1]上是“慢增函数”,下面的θ和正数b能满足的条件的是
(θ,b是常数)在(0,1]上是“慢增函数”,下面的θ和正数b能满足的条件的是
- A.b=-1,
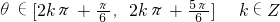
- B.
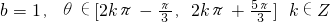
- C.b=2,
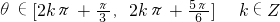
- D.
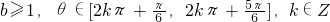
D
分析:由于h(x)在(0,1]上是“慢增函数”,所以h(x)在(0,1]上单调递增, 在(0,1]上单调递减,由此可求出θ及正数b满足的条件.
在(0,1]上单调递减,由此可求出θ及正数b满足的条件.
解答:因为h(x)=x2+(sinθ- )x+b(θ、b是常数)在(0,1]上是“慢增函数”
)x+b(θ、b是常数)在(0,1]上是“慢增函数”
所以h(x)=x2+(sinθ- )x+b在(0,1]上是增函数,
)x+b在(0,1]上是增函数,
且F(x)= =x+
=x+ +(sinθ-
+(sinθ- )在(0,1]上是减函数,
)在(0,1]上是减函数,
由h(x)=x2+(sinθ- )x+b在(0,1]上是增函数,得h′(x)≥0
)x+b在(0,1]上是增函数,得h′(x)≥0
即2x+(sinθ- )≥0在(0,1]上恒成立,
)≥0在(0,1]上恒成立,
所以 ≤0,
≤0,
即sinθ≥ ,
,
解得θ∈[2kπ+ ,2kπ+
,2kπ+ ],k∈Z.
],k∈Z.
由F(x)= 在(0,1]上是减函数,得F′(x)≤0在(0,1]上恒成立,
在(0,1]上是减函数,得F′(x)≤0在(0,1]上恒成立,
即1-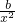 ≤0,b≥x2在(0,1]上恒成立,
≤0,b≥x2在(0,1]上恒成立,
所以b≥1.
综上所述,b≥1且θ∈[2kπ+ ,2kπ+
,2kπ+ ],k∈Z时,h(x)在(0,1]上是“慢增函数”.
],k∈Z时,h(x)在(0,1]上是“慢增函数”.
故选D
点评:本题以新定义的形式考查函数的单调性,考查运用所学知识分析解决新问题的能力.
分析:由于h(x)在(0,1]上是“慢增函数”,所以h(x)在(0,1]上单调递增,
 在(0,1]上单调递减,由此可求出θ及正数b满足的条件.
在(0,1]上单调递减,由此可求出θ及正数b满足的条件.解答:因为h(x)=x2+(sinθ-
 )x+b(θ、b是常数)在(0,1]上是“慢增函数”
)x+b(θ、b是常数)在(0,1]上是“慢增函数”所以h(x)=x2+(sinθ-
 )x+b在(0,1]上是增函数,
)x+b在(0,1]上是增函数,且F(x)=
 =x+
=x+ +(sinθ-
+(sinθ- )在(0,1]上是减函数,
)在(0,1]上是减函数,由h(x)=x2+(sinθ-
 )x+b在(0,1]上是增函数,得h′(x)≥0
)x+b在(0,1]上是增函数,得h′(x)≥0即2x+(sinθ-
 )≥0在(0,1]上恒成立,
)≥0在(0,1]上恒成立,所以
 ≤0,
≤0,即sinθ≥
 ,
,解得θ∈[2kπ+
 ,2kπ+
,2kπ+ ],k∈Z.
],k∈Z.由F(x)=
 在(0,1]上是减函数,得F′(x)≤0在(0,1]上恒成立,
在(0,1]上是减函数,得F′(x)≤0在(0,1]上恒成立,即1-
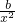 ≤0,b≥x2在(0,1]上恒成立,
≤0,b≥x2在(0,1]上恒成立,所以b≥1.
综上所述,b≥1且θ∈[2kπ+
 ,2kπ+
,2kπ+ ],k∈Z时,h(x)在(0,1]上是“慢增函数”.
],k∈Z时,h(x)在(0,1]上是“慢增函数”.故选D
点评:本题以新定义的形式考查函数的单调性,考查运用所学知识分析解决新问题的能力.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目