题目内容
已知等差数列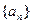 的前
的前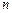 项和为
项和为 ,且
,且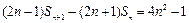
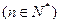 .
.
(Ⅰ)求数列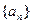 的通项公式;
的通项公式;
(Ⅱ)求证: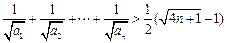
 的前
的前 项和为
项和为 ,且
,且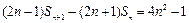
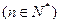 .
.(Ⅰ)求数列
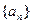 的通项公式;
的通项公式;(Ⅱ)求证:
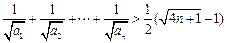
(Ⅰ)由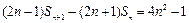 ,得
,得 ,
,
∴ 是公差为1的等差数列,
是公差为1的等差数列,
∴ ,
, ①
①
又∵ 等差数列,∴
等差数列,∴ ,即
,即 .
.
由①得 ,
,
解得 ,代入①得
,代入①得 .
.
当 时,
时,
 ,
,
上式对 也适用,∴
也适用,∴
 .
.
(Ⅱ)由(Ⅰ)知,

 ,
,
∴

 ,故原不等式成立.
,故原不等式成立.
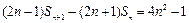 ,得
,得 ,
,∴
 是公差为1的等差数列,
是公差为1的等差数列, ∴
 ,
, ①
①
又∵
 等差数列,∴
等差数列,∴ ,即
,即 .
.由①得
 ,
,解得
 ,代入①得
,代入①得 .
. 当
 时,
时,
 ,
,上式对
 也适用,∴
也适用,∴
 .
. (Ⅱ)由(Ⅰ)知,


 ,
, ∴


 ,故原不等式成立.
,故原不等式成立. 略

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 满足
满足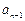 +
+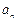 =4n-3(n∈
=4n-3(n∈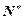 ).
).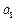 的值;
的值;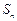 ;
;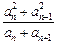 ≥5成立,求
≥5成立,求 ,数列
,数列 满足
满足 ,
, ,
,
 I)求证数列
I)求证数列 是等比数列;
是等比数列; 中最大项
中最大项




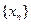 满足:
满足: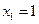 ,
, .
.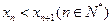 ;
;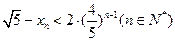

 的前n项和
的前n项和 ,第k项满足
,第k项满足 ,则k等于( )
,则k等于( ) 是一个等差数列﹐且满足
是一个等差数列﹐且满足 及
及 ﹒若定义函数
﹒若定义函数 ,其中
,其中 ﹐则下列命题中错误的是( )
﹐则下列命题中错误的是( )

 为递增函数
为递增函数 ,不等式
,不等式 恒成立.
恒成立. }的前n项和为
}的前n项和为 ,a3=20,S3=36,则
,a3=20,S3=36,则 +
+ +
+ +…+
+…+ =___.
=___.