题目内容
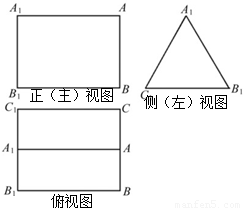
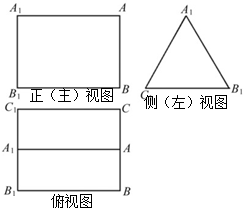 如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.
如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.(1)求证:AB1∥平面BDC1;
(2)设AB1垂直于BC1,且BC=2,求点C到平面DBC1的距离.
分析:(1)利用线线平行证明线面平行即可;
(2)先作出直线AB1在平面BCC1B1内的射影,利用平面几何知识求出BB1的长,再利用三棱锥的换底性,用等体积法求解即可.
(2)先作出直线AB1在平面BCC1B1内的射影,利用平面几何知识求出BB1的长,再利用三棱锥的换底性,用等体积法求解即可.
解答:解:(1)证明:几何体的直观图,如图,
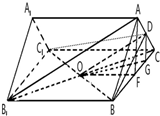
连接BC1和B1C,交点为O,则O为B1C的中点,连接OD,
∵D为中点,∴OD∥AB1,
又AB1?平面BDC1,OD?平面ABC1,
∴AB1∥平面BDC1.
(2)过D作DG⊥BC,垂足为G,连接GO,
∵侧面垂直于底面,∴DG⊥侧面BCC1B1,
∴OD在侧面BCC1B1内的射影为GO,
∵BC=2,△ABC为等边三角形,∴DG=
,
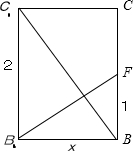
连接B1F,则B1F为AB1在侧面BCC1B1内的射影,
∵AB1⊥BC1,由三垂线逆定理得B1F⊥BC1,如图:
设BB1=x,∵∠FB1B=∠BC1B1,∴
=
,∴BB1=
,
S△CBC1=
×2×
,
∵BD=
,DC1=
,BC1=
,∴BD⊥DC1,
∴S△DBC1=
×
×
用等体积法VC-DBC1=VD-CBC1⇒h=
=
.

连接BC1和B1C,交点为O,则O为B1C的中点,连接OD,
∵D为中点,∴OD∥AB1,
又AB1?平面BDC1,OD?平面ABC1,
∴AB1∥平面BDC1.
(2)过D作DG⊥BC,垂足为G,连接GO,
∵侧面垂直于底面,∴DG⊥侧面BCC1B1,
∴OD在侧面BCC1B1内的射影为GO,
∵BC=2,△ABC为等边三角形,∴DG=
| ||
| 2 |
连接B1F,则B1F为AB1在侧面BCC1B1内的射影,
∵AB1⊥BC1,由三垂线逆定理得B1F⊥BC1,如图:
设BB1=x,∵∠FB1B=∠BC1B1,∴
| 1 |
| x |
| x |
| 2 |
| 2 |
S△CBC1=
| 1 |
| 2 |
| 2 |
∵BD=
| 3 |
| 3 |
| 6 |
∴S△DBC1=
| 1 |
| 2 |
| 3 |
| 3 |
用等体积法VC-DBC1=VD-CBC1⇒h=
| SCBC1DG |
| SDBC1 |
| ||
| 3 |

点评:本题考查线面平行的判定,点到平面距离的求法.等体积法求点到面的距离的常用方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
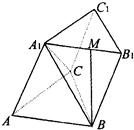 如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧面ABB1A1是菱形且垂直于底面,∠A1AB=60°,M是A1B1的中点.
如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧面ABB1A1是菱形且垂直于底面,∠A1AB=60°,M是A1B1的中点.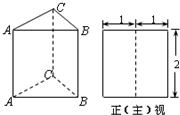 如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正视图是边长为2的正方形,则此三棱柱侧视图的面积为( )
如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正视图是边长为2的正方形,则此三棱柱侧视图的面积为( ) (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=