题目内容
如图所示,扇形OAB的半径为2,圆心角为| π | 3 |
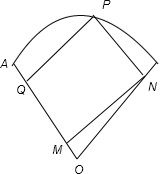
分析:设∠AOP=α,进而可表示出PQ和PN,进而利用矩形面积公式表示出矩形的面积,利用积化和差公式整理,根据余弦函数的性质求得面积的最大值.
解答:解:连接OP,设∠AOP=α
PQ=2sinα PN=2sin(
-α)
S=PQ•PN=4•sina•sin(
-α)
=4×
×[cos(2α-
)-cos
]
=2cos(2α-
)-1
所以α=
的时候最大,S=1
PQ=2sinα PN=2sin(
| π |
| 3 |
S=PQ•PN=4•sina•sin(
| π |
| 3 |
=4×
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
=2cos(2α-
| π |
| 3 |
所以α=
| π |
| 6 |
点评:本题主要考查了三角函数的最值问题.考查了学生综合运用所学知识解决实际问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
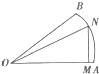 如图所示,某城镇为适应旅游产业的需要,欲在一扇形OAB(其中∠AOB=45°,扇形半径为1)草地上修建一个三角形人造湖OMN(其中M在OA上,N在
如图所示,某城镇为适应旅游产业的需要,欲在一扇形OAB(其中∠AOB=45°,扇形半径为1)草地上修建一个三角形人造湖OMN(其中M在OA上,N在
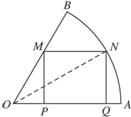






 ,P为圆弧AB上的一点,试问P点在何处时,矩形PQMN的面积S最大.
,P为圆弧AB上的一点,试问P点在何处时,矩形PQMN的面积S最大.