题目内容
以100元/件的价格购进一批羊毛衫,以高于进价的相同价格出售.羊毛衫的销售有淡季与旺季之分.标价越高,购买人数越少.我们称刚好无人购买时的最低标价为羊毛衫的最高价格.某商场经销某品牌的羊毛衫,无论销售淡季还是旺季,进货价都是100/件.针对该品牌羊毛衫的市场调查显示:
①购买该品牌羊毛衫的人数是标价的一次函数;
②该品牌羊毛衫销售旺季的最高价格是淡季最高价格的 倍;
倍;
③在销售旺季,商场以140元/件价格销售时能获取最大利润.
(I)分别求该品牌羊毛衫销售旺季的最高价格与淡季最高价格;
(II)问:在淡季销售时,商场要获取最大利润,羊毛衫的标价应定为多少.
则旺季的最高价格为-
 元/件,利润函
元/件,利润函L(x)=(x-100)•(kx+b)=kx2-(100k-b)-100b,x∈[100,-
 ],
],当x=
 =50-
=50- 时,L(x)最大,由题意知,50-
时,L(x)最大,由题意知,50- =140,解得-
=140,解得- =180,
=180,即旺季的最高价格是180(元/件),则淡季的最高价格是180×
 =120(元/件).
=120(元/件).(II)现设淡季销售时,羊毛衫的标价为t元/件,购买人数为mt+n(m<0),
则淡季的最高价格为-
 =120(元/件),即n=-120m,
=120(元/件),即n=-120m,利润函数L(t)=(t-100)•(mt+n)=(t-100)•(mt-120m)
=-m(t-100)•(120-t),t∈[100,120].
∴t-100=120-t,即t=110时,L(t)为最大,
∴在淡季销售时,商场要获取最大利润,羊毛衫的标价应定为110元/件.
分析:(I)设在旺季销售时,羊毛衫的标价为x元/件,购买人数为kx+b(k<0),则旺季的最高价格为-
 元/件,从而求出利润函,利用二次函数在闭区间[100,-
元/件,从而求出利润函,利用二次函数在闭区间[100,- ]上求出最值即可求出所求;
]上求出最值即可求出所求;(II)现设淡季销售时,羊毛衫的标价为t元/件,购买人数为mt+n(m<0),则淡季的最高价格为-
 =120(元/件),得m与n的关系,从而得到利润函数L(t),求出最大值即可.
=120(元/件),得m与n的关系,从而得到利润函数L(t),求出最大值即可.点评:本题主要考查了函数模型的选择与应用,以及二次函数在实际生活中的应用,解题的关键是理解题意,找到等量关系,属于中档题.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案(本小题满分12分)某商场以100元/件的价格购进一批衬衣,以高于进价的价格出售,销售有淡季旺季之分.通过市场调查发现:①销售量![]() (件)与衬衣标价x(元/件)在销售旺季近似地符合函数关系:
(件)与衬衣标价x(元/件)在销售旺季近似地符合函数关系:![]() ;在销售淡季近似地符合函数关系:
;在销售淡季近似地符合函数关系:![]() 、
、![]() 、
、![]() 、
、![]() 为常数;②在销售旺季,商场以140元/件的价格销售能获得最大销售利润;③若称①中
为常数;②在销售旺季,商场以140元/件的价格销售能获得最大销售利润;③若称①中![]() 时的标价x为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.
时的标价x为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.
请根据上述信息,完成下面问题:
(Ⅰ)填出表格中空格的内容;
| 数量关系 销售季节 | 标价 (元/件) | 销售量 (含k、b1或b2) | 不同季节的销售总利润y(元) 与标价x(元/件)的函数关系式 |
| 旺 季 | x |
| |
| 淡 季 | x |
(Ⅱ)在销售淡季,该商场要获得最大销售利润,衬衣的标价应定为多少元才合适?
(本小题满分12分)某商场以100元/件的价格购进一批衬衣,以高于进价的价格出售,销售有淡季旺季之分.通过市场调查发现:①销售量![]() (件)与衬衣标价x(元/件)在销售旺季近似地符合函数关系:
(件)与衬衣标价x(元/件)在销售旺季近似地符合函数关系:![]() ;在销售淡季近似地符合函数关系:
;在销售淡季近似地符合函数关系:![]() 、
、![]() 、
、![]() 、
、![]() 为常数;②在销售旺季,商场以140元/件的价格销售能获得最大销售利润;③若称①中
为常数;②在销售旺季,商场以140元/件的价格销售能获得最大销售利润;③若称①中![]() 时的标价x为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.
时的标价x为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.
请根据上述信息,完成下面问题:
(Ⅰ)填出表格中空格的内容;
| 数量关系 销售季节 | 标价 (元/件) | 销售量 (含k、b1或b2) | 不同季节的销售总利润y(元) 与标价x(元/件)的函数关系式 |
| 旺 季 | x |
| |
| 淡 季 | x |
(Ⅱ)在销售淡季,该商场要获得最大销售利润,衬衣的标价应定为多少元才合适?
(本小题满分14分)
某商场以100元/件的价格购进一批衬衣,以高于进货价的价格出售,销售期有淡季与旺季之分,通过市场调查发现:
①销售量 (件)与衬衣标价
(件)与衬衣标价 (元/件)在销售旺季近似地符合函数关系:
(元/件)在销售旺季近似地符合函数关系: ,在销售淡季近似地符合函数关系:
,在销售淡季近似地符合函数关系: ,其中
,其中 为常数;
为常数;
②在销售旺季,商场以140元/件的价格销售能获得最大销售利润;
③若称①中 时的标价
时的标价 为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.
为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.
请根据上述信息,完成下面问题:
(Ⅰ)填出表格中空格的内容:
|
销售关系 |
标价(元/件) |
销售量 |
销售总利润 (元/件)的函数关系式 |
|
旺季 |
|
|
|
|
淡季 |
|
|
|
(Ⅱ)在销售淡季,该商场要获得最大销售利润,衬衣的标价应定为多少元/件?
 数量关系
数量关系 、
、 或
或 )
)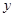 (元)与标价
(元)与标价