题目内容
若不等式ax2+bx+c>0的解集为{x|-3<x<4},求不等式bx2+2ax-c-3b<0的解集.
思路分析:根据已知解集和一元二次不等式解的结构逆向推出a、b、c应满足的关系,进而求解不等式.
解:∵ax2+bx+c>0的解集为{x|-3<x<4},
∴a<0且-3和4是方程ax2+bx+c=0的两根.
由韦达定理得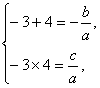
即![]()
∴不等式bx2+2ax-c-3b<0,
即为-ax2+2ax+15a<0,
即x2-2x-15<0.
故所求的不等式的解集为{x|-3<x<5}.

练习册系列答案
相关题目