题目内容
设函数f(x)= ,给定数列{an},其中a1=a,an+1=f(an)(n∈N*).
,给定数列{an},其中a1=a,an+1=f(an)(n∈N*).
(1)若{an}为常数数列,求a的值;
(2)当a≠0时,探究{ +2}能否是等比数列?若是,求出{an}的通项公式;若不是,说明理由;
+2}能否是等比数列?若是,求出{an}的通项公式;若不是,说明理由;
(3)设bn=3nan,数列{bn}的前n项和为Sn,当a=1时,求证:Sn>4-(n+2)( )n-1.
)n-1.
解:(1)若{an}为常数数列,则an=a,由an+1=f(an),得a=f(a),(1分)
f(x)= ,∴
,∴ ,即a=2a(a+1)解得:a=0或
,即a=2a(a+1)解得:a=0或 .
.
(2)∵f(x)= ,∴an+1=f(an)=
,∴an+1=f(an)= ,
,
当a1=a≠0时,an≠0,
∴ ,
,
∴ ,
,
∴ +2=
+2= +2,…(6分)
+2,…(6分)
∴①当a=- 时,由(1)知
时,由(1)知 ,∴
,∴ 不是等比数列.…(7分)
不是等比数列.…(7分)
②当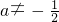 时,
时, ,∴
,∴ 是以2为公比,以
是以2为公比,以 为首项的等比数列,…(8分)
为首项的等比数列,…(8分)
∴ ,∴
,∴ …(9分)
…(9分)
(3)当a=1时, ,…(10分)
,…(10分)
∴
∴ …(11分)
…(11分)
设 ①
①
则 ,②
,②
由①-②得:
=
∴ ,(13分),
,(13分),
所以 …(14分)
…(14分)
分析:(1)由于a1=a,{an}为常数数列,得知a=f(a),将其代入f(x)= ,从而求出a的值;
,从而求出a的值;
(2)根据an+1=f(an)取倒数化简得 ,再考虑首项是否为0分类讨论,它是否是等比数列.
,再考虑首项是否为0分类讨论,它是否是等比数列.
(3)根据(2)得a=1时,它是等比数列,从而求出an的通项公式,并放缩,得 ,
,
∴ ,令右式=Tn,再用错位相减法化简右式得Tn=
,令右式=Tn,再用错位相减法化简右式得Tn= ,从而得证.
,从而得证.
点评:此题考查等比数列的判断,关键在于其首项是否为0,比值是否为常数.同时还考查了放缩法及数列求和的错位相减法.
f(x)=
 ,∴
,∴ ,即a=2a(a+1)解得:a=0或
,即a=2a(a+1)解得:a=0或 .
.(2)∵f(x)=
 ,∴an+1=f(an)=
,∴an+1=f(an)= ,
,当a1=a≠0时,an≠0,
∴
 ,
,∴
 ,
,∴
 +2=
+2= +2,…(6分)
+2,…(6分)∴①当a=-
 时,由(1)知
时,由(1)知 ,∴
,∴ 不是等比数列.…(7分)
不是等比数列.…(7分)②当
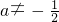 时,
时, ,∴
,∴ 是以2为公比,以
是以2为公比,以 为首项的等比数列,…(8分)
为首项的等比数列,…(8分)∴
 ,∴
,∴ …(9分)
…(9分)(3)当a=1时,
 ,…(10分)
,…(10分)∴

∴
 …(11分)
…(11分)设
 ①
①则
 ,②
,②由①-②得:

=

∴
 ,(13分),
,(13分),所以
 …(14分)
…(14分)分析:(1)由于a1=a,{an}为常数数列,得知a=f(a),将其代入f(x)=
 ,从而求出a的值;
,从而求出a的值;(2)根据an+1=f(an)取倒数化简得
 ,再考虑首项是否为0分类讨论,它是否是等比数列.
,再考虑首项是否为0分类讨论,它是否是等比数列.(3)根据(2)得a=1时,它是等比数列,从而求出an的通项公式,并放缩,得
 ,
,∴
 ,令右式=Tn,再用错位相减法化简右式得Tn=
,令右式=Tn,再用错位相减法化简右式得Tn= ,从而得证.
,从而得证.点评:此题考查等比数列的判断,关键在于其首项是否为0,比值是否为常数.同时还考查了放缩法及数列求和的错位相减法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目