题目内容
已知函数f(x)= ,若对于任意的x∈N*,f(x)≥3恒成立,则a 的最小值等于
,若对于任意的x∈N*,f(x)≥3恒成立,则a 的最小值等于
- A.
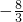
- B.-3
- C.

- D.-6
A
分析:f(x)=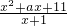 ≥3恒成立,即x2+ax+11≥3x+3恒成立,再分离参数求最值,即可得到结论.
≥3恒成立,即x2+ax+11≥3x+3恒成立,再分离参数求最值,即可得到结论.
解答:∵x∈N*,
∴f(x)=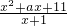 ≥3恒成立,即x2+ax+11≥3x+3恒成立,
≥3恒成立,即x2+ax+11≥3x+3恒成立,
∴ax≥-x2-8+3x,又x∈N*,
∴a≥- -x+3恒成立,
-x+3恒成立,
令g(x)=- -x+3(x∈N*),∴a≥g(x)max,
-x+3(x∈N*),∴a≥g(x)max,
再令h(x)=x+ (x∈N*),
(x∈N*),
∵h(x)=x+ 在(0,2
在(0,2 ]上单调递减,在[2
]上单调递减,在[2 ,+∞)上单调递增,而x∈N*,
,+∞)上单调递增,而x∈N*,
∴h(x)在x取距离2 较近的整数值时达到最小,而距离2
较近的整数值时达到最小,而距离2 较近的整数为2和3,
较近的整数为2和3,
∵h(2)=6,h(3)= ,h(2)>h(3),
,h(2)>h(3),
∴当x∈N*时,h(x)min= .又g(x)=-
.又g(x)=- -x+3=-h(x)+3,
-x+3=-h(x)+3,
∴g(x)max=- +3=-
+3=- .
.
∴a≥- .
.
故选A.
点评:本题考查函数恒成立问题,考查转化思想,构造函数的思想,考查函数的单调性的应用,综合性强,属于中档题.
分析:f(x)=
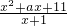 ≥3恒成立,即x2+ax+11≥3x+3恒成立,再分离参数求最值,即可得到结论.
≥3恒成立,即x2+ax+11≥3x+3恒成立,再分离参数求最值,即可得到结论.解答:∵x∈N*,
∴f(x)=
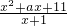 ≥3恒成立,即x2+ax+11≥3x+3恒成立,
≥3恒成立,即x2+ax+11≥3x+3恒成立,∴ax≥-x2-8+3x,又x∈N*,
∴a≥-
 -x+3恒成立,
-x+3恒成立,令g(x)=-
 -x+3(x∈N*),∴a≥g(x)max,
-x+3(x∈N*),∴a≥g(x)max,再令h(x)=x+
 (x∈N*),
(x∈N*),∵h(x)=x+
 在(0,2
在(0,2 ]上单调递减,在[2
]上单调递减,在[2 ,+∞)上单调递增,而x∈N*,
,+∞)上单调递增,而x∈N*,∴h(x)在x取距离2
 较近的整数值时达到最小,而距离2
较近的整数值时达到最小,而距离2 较近的整数为2和3,
较近的整数为2和3,∵h(2)=6,h(3)=
 ,h(2)>h(3),
,h(2)>h(3),∴当x∈N*时,h(x)min=
 .又g(x)=-
.又g(x)=- -x+3=-h(x)+3,
-x+3=-h(x)+3,∴g(x)max=-
 +3=-
+3=- .
.∴a≥-
 .
.故选A.
点评:本题考查函数恒成立问题,考查转化思想,构造函数的思想,考查函数的单调性的应用,综合性强,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|