题目内容
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,直线l:x+2y=4与椭圆有且只有一个交点T.
,直线l:x+2y=4与椭圆有且只有一个交点T.
(I)求椭圆C的方程和点T的坐标;
(Ⅱ)O为坐标原点,与OT平行的直线l′与椭圆C交于不同的两点A,B,直线l′与直线l交于点P,试判断![]() 是否为定值,若是请求出定值,若不是请说明理由.
是否为定值,若是请求出定值,若不是请说明理由.
【答案】(I)![]() +
+![]() =1,T(1,
=1,T(1,![]() ); (Ⅱ)见解析.
); (Ⅱ)见解析.
【解析】
(I)由椭圆的离心率为![]() 得到 b2=
得到 b2=![]() a2,根据直线l:x+2y=4与椭圆有且只有一个交点T得到△=0,解得a2=4,b2=3,即得椭圆的方程. (Ⅱ)先计算出|PT|2=
a2,根据直线l:x+2y=4与椭圆有且只有一个交点T得到△=0,解得a2=4,b2=3,即得椭圆的方程. (Ⅱ)先计算出|PT|2=![]() t2,|PA|=
t2,|PA|=![]() =
=![]() |
|![]() ﹣x1|,|PB|=
﹣x1|,|PB|=![]() |
|![]() ﹣x2|,再计算
﹣x2|,再计算![]() =
=![]() 为定值.
为定值.
(I)由椭圆的离心率e=![]() =
=![]() =
=![]() ,则b2=
,则b2=![]() a2,
a2,
则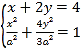 ,消去x,整理得:
,消去x,整理得:![]() y2﹣16y+16﹣a2=0,①
y2﹣16y+16﹣a2=0,①
由△=0,解得:a2=4,b2=3,
所以椭圆的标准方程为:![]() +
+![]() =1;所以
=1;所以![]() =
=![]() ,则T(1,
,则T(1,![]() ),
),
(Ⅱ)设直线l′的方程为y=![]() x+t,由
x+t,由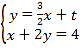 ,解得P的坐标为(1﹣
,解得P的坐标为(1﹣![]() ,
,![]() +
+![]() ),
),
所以|PT|2=![]() t2,
t2,
设设A(x1,y1),B(x2,y2),联立 ,消去y整理得x2+tx+
,消去y整理得x2+tx+![]() ﹣1=0,
﹣1=0,
则x1+x2=﹣t,x1x2=![]() ,△=t2﹣4(
,△=t2﹣4(![]() ﹣1)>0,t2<12,
﹣1)>0,t2<12,
y1=![]() x1+t,y2=
x1+t,y2=![]() x2+t,|PA|=
x2+t,|PA|=![]() =
=![]() |
|![]() ﹣x1|,
﹣x1|,
同理|PB|=![]() |
|![]() ﹣x2|,
﹣x2|,
|PA||PB|=![]() |(
|(![]() ﹣x1)(
﹣x1)(![]() ﹣x2)|=
﹣x2)|=![]() |
|![]() ﹣
﹣![]() (x1+x2)+x1x2|,
(x1+x2)+x1x2|,
![]() |
|![]() ﹣
﹣![]() (﹣t)+
(﹣t)+![]() |=
|=![]() t2,所以
t2,所以![]() =
=![]() =
=![]() ,
,
所以![]() =
=![]() 为定值.
为定值.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目