题目内容
已知函数
（m为常数，且m>0）有极大值9.
（Ⅰ）求m的值；
（Ⅱ）若斜率为-5的直线是曲线
的切线，求此直线方程.
解：(Ⅰ) 
则
或
当x变化时，
与
的变化情况如下表：
| x | (－∞,－m) | －m | (－m, |
| ( |
| f’(x) | + | 0 | － | 0 | + |
| f (x) |
| 极大值 | 极小值 |
)
从而可知，当x=－m时，函数f(x)取得极大值9，
即
＝－m3+m3+m3+1=9,∴m＝2.
(Ⅱ)由(Ⅰ)知， =x3+2x2－4x+1,
依题意知＝3x2＋4x－4＝－5，∴x＝－1或x＝
又
，
，
所以切线方程为y－6＝－5(x＋1),或y－
＝－5(x＋
)，
即5x＋y－1＝0，或135x＋27y－23＝0.
练习册系列答案
相关题目
（m为常数，且m>0）有极大值9.
的切线，求此直线方程.
（m为常数,e=2.71828…是自然对数的底数），函数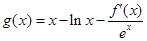
的最小值为1，其中
是函数f(x)的导数.
（m为常数)，对任意的 
恒成立.有下列说法：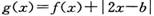
(b为常数)的图象关于直线x=1对称，则b=1;
成立，且当
时，
；又函数
(c为常数），若存在
使得
成立，则c的取值范围是(一1，13).
（m为常数，m>0）有极大值9.
的切线，求此直线方程.
（m为常数，且m>0）有极大值9．
的直线是曲线
的切线，求此直线方程．