题目内容
(不等式选讲选做题)若关于x的不等式|x+1|-|x-2|>
存在实数解,则实数a的取取值范围是 .
| 1 | a |
分析:令f(x)=|x+1|-|x-2|,则f(x)=
,如图所示.由于关于x的不等式|x+1|-|x-2|>
存在实数解?
<f(x)max,解出即可.
|
| 1 |
| a |
| 1 |
| a |
解答:解:令f(x)=|x+1|-|x-2|,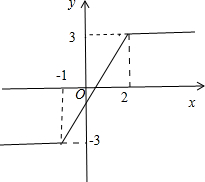
则f(x)=
,如图所示.
∵关于x的不等式|x+1|-|x-2|>
存在实数解,
∴
<f(x)max=3,
解得a<0或a>
,
故a的取值范围是(-∞,0)∪(
,+∞).
故答案为(-∞,0)∪(
,+∞).

则f(x)=
|
∵关于x的不等式|x+1|-|x-2|>
| 1 |
| a |
∴
| 1 |
| a |
解得a<0或a>
| 1 |
| 3 |
故a的取值范围是(-∞,0)∪(
| 1 |
| 3 |
故答案为(-∞,0)∪(
| 1 |
| 3 |
点评:本题考查了含绝对值的不等式的恒成立问题的等价转化、数形结合等基础知识与基本技能方法,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
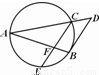
 ,则线段CD的长为 .
,则线段CD的长为 .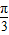 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .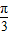 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .