Question

已知函数f(x)=(x²-2ax)e^x,x∈R,a∈R.

（1）当a≥0时,f(x)是否存在最小值,若存在,请求出相应x的值；若不存在,请说明理由.

（2）当x∈［-2,］时,若f(x)的图象上存在两点M,N,使得直线MN⊥y轴，求实数a的取值范围.

Answer 1

解:(1)∵f′(x)=(x²+2x-2ax-2a)e^x,令f′(x)=0,即x²+2(1-a)x-2a=0,

解得x₁=a-1-,x₂=a-1+.2分∵a≥0,∴x₁＜-1,x₂≥0.

当x＜x₁或x＞x₂时,f′(x)＞0;当x₁＜x＜x₂时,f′(x)＜0,

∴f(x)在(-∞,x₁)和(x₂,+∞)上单调递增,在(x₁,x₂)上单调递减.

∴f(x)在x₁处取极大值,在x₂处取得极小值.

又∵当x=0时,f(x)=0;当x＜0时,f(x)=x(x-2a)e^x＞0,

∴x∈(-∞,a-1-)时,f(x)∈(0,f(a-1-)).x∈(a-1-,a-1+)时,

f(x)∈(f(a-1-),f(a-1+));

x∈(a-1+,+∞)时,f(x)∈(f(a-1+),+∞),

又f(a-1+)=(2-2)≤0,

∴x=a-1+时，f(x)取得最小值.

(2)∵x∈［-2,］时f(x)的图象上存在两点M,N,使得直线MN⊥y轴,则x∈［-2,］时f(x)不是单调增函数,也不是单调减函数,∴f′(x)=(x²+2x-2ax-2a)e^x在x∈［-2,］上有正有负.∴g(x)=x²+2x-2ax-2a在x∈［-2,］上有正有负.

而g(-1)=1-2+2a-2a=-1＜0,∴g(x)=x²+2x-2ax-2a在x∈［-2,］上有正有负的充要条件为

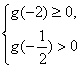g(-2)g()＜0或或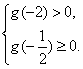

由g(-2)g()＜0,解得a＞0或a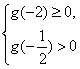＜;或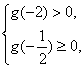解得a不存在.

综上,a的取值范围是a＞0或a＜.

注:(1)若学生从反面考虑,先求得函数f(x)单调时a的范围≤a≤0,再求其补集也可;

(2)若学生求出f′(x)=0的根x₁=a-1,x₂=a-1+,

利用-2＜a-1-a²+1＜或-2＜a-1+a²+1＜,

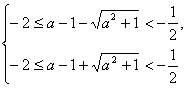或或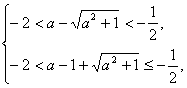解得a＞0或a＜也可.

(3)若学生未发现g(-1)＜0,直接从“Δ”、“对称轴”、“端点函数值”综合考虑也可.