题目内容
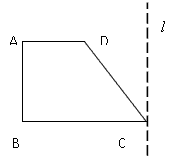
如图，已知梯形ABCD满足AD∥BC，AD⊥DB，且∠ABD=∠BCD=
，DB=
，现将△DBC绕D点顺时针旋转α角（0＜α＜
）后得△DB1C1，DC1交BC于点E，DB1交AB于点F．当DF=1时，求α的值．
解：∵梯形ABCD满足AD∥BC，AD⊥DB，
∴∠ADB=∠DBC=90°
在RT△ADB中，DB=，∠ABD=，∴AD=1，∴∠DAB=，
又∵DF=1，∴△ADF为等边三角形，
∴∠ADF=，
∴α=
分析：先确定AD=1，∠DAB=，根据DF=1，可得△ADF为等边三角形，因此可求α的值．
点评：本题考查图形的旋转，考查学生的计算能力，属于基础题．
∴∠ADB=∠DBC=90°
在RT△ADB中，DB=
，∠ABD=，∴AD=1，∴∠DAB=，又∵DF=1，∴△ADF为等边三角形，
∴∠ADF=
，∴α=
分析：先确定AD=1，∠DAB=
，根据DF=1，可得△ADF为等边三角形，因此可求α的值．点评：本题考查图形的旋转，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
如图，已知梯形ABCD中，AD∥BC，∠ABC=90°，AD=a，BC=2a，∠DCB=60°，在平面ABCD内，过C作l⊥CB，以l为轴将梯形ABCD旋转一周，求所得旋转体的表面积及体积．
＝λ
(λ∈R，λ＞0)．
时，求证：GM∥平面DFN．
，试求二面角M－BC－D的余弦值．
为矩阵
属于λ的一个特征向量，求实数a，λ的值及A2。
（α为参数），曲线D的参数方程为
，（t为参数）。若曲线C、D有公共点，求实数m的取值范围。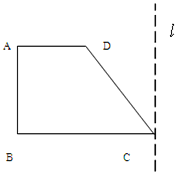
如图，已知梯形ABCD中，AD∥BC，∠ABC=90°，AD=a，BC=2a，∠DCB=60°，在平面ABCD内，过C作l⊥CB，以l为轴将梯形ABCD旋转一周，求所得旋转体的表面积及体积．