题目内容
关于下列命题：
①函数y=tanx在第一象限是增函数；
②函数y=cos2（
-x）是偶函数；
③函数y=4sin（2x-
）的一个对称中心是（
，0）；
④函数y=sin（x+
）在闭区间[-
，
]上是增函数．
写出所有正确的命题的题号：______．
①函数y=tanx在第一象限是增函数；
②函数y=cos2（
| π |
| 4 |
③函数y=4sin（2x-
| π |
| 3 |
| π |
| 6 |
④函数y=sin（x+
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
写出所有正确的命题的题号：______．
①函数y=tanx在第一象限是增函数；显然不正确，正切函数在类似[0，
）上是增函数，第一象限是增函数，错误．
②函数y=cos2(
-x)=sin2x是偶函数，是错误的；
③因为x=
时，函数y=4sin(2x-
)=0，所以函数y=4sin(2x-
)的一个对称中心是（
，0）；正确．
④函数y=sin(x+
)在闭区间[-
，
]上是增函数．这是不正确的．在[-
，
]上函数有增有减．
故答案为：③
| π |
| 2 |
②函数y=cos2(
| π |
| 4 |
③因为x=
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
④函数y=sin(x+
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故答案为：③
练习册系列答案
寒假学与练系列答案
相关题目
在第一象限是增函数；
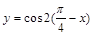是奇函数；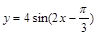 
的一个对称中心是（
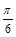，0）；
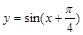在闭区间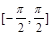
上是增函数.
在第一象限是增函数；②函数
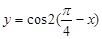是偶函数；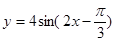 
的一个对称中心是（
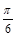，0）；
在闭区间
上是增函数;