题目内容

如图，AB是⊙O的直径，CD是⊙O的切线，C是切点，AD交⊙O于点E，AC=，CD=1，AC平分∠BAA。

（1）求证：AD⊥CD；

（2）求AB的长。

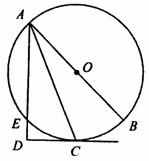
解：（1）连结BC

∵AB是⊙O的直径，

∴∠ACB=90°。

∵CD是⊙O的切线，AD交⊙O于点E，

∴∠ACD=∠ABC。

∵AC平分∠BAD

∴∠CAD=∠BAC。

∴△ACD∽△ABC

∴∠ADC=∠ACB=90°

∴AD⊥CD。

（2）∵△ACD∽△ABC

∴

∵AC=

∴AD=2

∴

练习册系列答案
相关题目
（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A1B1C1D1，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．
精英家教网
（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．
精英家教网

如图，已知PA垂直于⊙O所在平面，AB是⊙O的直径，点C为圆周上异于A、B的一点．

(1)若一个n面体中有m个面是直角三角形，则称这个n面体的直度为．那么四面体P－ABC的直度为多少？说明理由；

(2)在四面体P－ABC中，AP＝AB＝1，设．若动点M在四面体P－ABC表面上运动，并且总保持PB⊥AM．设为动点M的轨迹围成的封闭图形的面积关于角的函数，求取最大值时，二面角A－PB－C的正切值．

如图，已知PA垂直于⊙O所在平面，AB是⊙O的直径，点C为圆周上异于A、B的一点．

(1)若一个n面体中有m个面是直角三角形，则称这个n面体的直度为．那么四面体P－ABC的直度为多少？说明理由；

(2)如图，若四面体P－ABC中，AP＝AB＝1，AE⊥PB，垂足为E，AF⊥PC，垂足为F．设∠EAF＝，为△AEF面积的函数，求取最大值时二面角A－PB－C的大小．
如图，ABCD是正方形，E、F分别是AD、BC边上的点，EF∥AB，EF交AC于点O，以EF为棱把它折成直二面角A-EF-D后，求证：不论EF怎样移动，∠AOC是定值.

 如图甲，已知PA垂直于⊙O所在平面，AB是⊙O的直径，点C为圆周上异于A、B的一点．

（1）若一个面体中有个面是直角三角形，则称这个面体的直度为．那么四面体的直度为多少？说明理由；

（2）在四面体中，，设．若动点在四面体 表面上运动，并且总保持．设为动点的轨迹围成的封闭图形的面积关于角的函数，求取最大值时,二面角的正切值．

 

 

 

 

 

 

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网