题目内容
已知数列{an}的前n项和为Sn,a1=- ,Sn+
,Sn+ =an-2(n≥2,n∈N)
=an-2(n≥2,n∈N)
(1)求S2,S3,S4的值;
(2)猜想Sn的表达式;并用数学归纳法加以证明.
解:(1)S1=a1=- ,∵Sn+
,∵Sn+ =an-2(n≥2,n∈N),令n=2可得
=an-2(n≥2,n∈N),令n=2可得
,S2+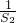 =a2-2=S2-a1-2,∴
=a2-2=S2-a1-2,∴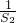 =
= -2,∴S2=-
-2,∴S2=- .
.
同理可求得 S3=- ,S4=-
,S4=- .
.
(2)猜想Sn =- ,n∈N+,下边用数学归纳法证明:
,n∈N+,下边用数学归纳法证明:
①当n=2时,S2=a1+a2=- ,猜想成立.
,猜想成立.
②假设当n=k时猜想成立,即SK=-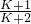 .
.
则当n=k+1时,∵Sn+ =an-2,∴
=an-2,∴ ,
,
∴ ,∴
,∴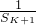 =
=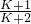 -2=
-2=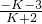 ,
,
∴SK+1=-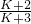 ,∴当n=k+1时,猜想仍然成立.
,∴当n=k+1时,猜想仍然成立.
综合①②可得,猜想对任意正整数都成立,即 Sn =- ,n∈N+成立.
,n∈N+成立.
分析:(1)S1=a1,由S2+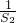 =a2-2=S2-a1 求得S2,同理求得 S3,S4.
=a2-2=S2-a1 求得S2,同理求得 S3,S4.
(2)猜想Sn =- ,n∈N+,用数学归纳法证明,检验n=1时,猜想成立;假设SK=-
,n∈N+,用数学归纳法证明,检验n=1时,猜想成立;假设SK=-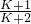 ,则当n=k+1时,由条件可得,
,则当n=k+1时,由条件可得, ,解出 SK+1=-
,解出 SK+1=-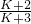 ,故n=k+1时,猜想仍然成立.
,故n=k+1时,猜想仍然成立.
点评:本题考查归纳推理,用数学归纳法证明等式,证明当n=k+1时,Sn =- ,n∈N+,是解题的难点.
,n∈N+,是解题的难点.
 ,∵Sn+
,∵Sn+ =an-2(n≥2,n∈N),令n=2可得
=an-2(n≥2,n∈N),令n=2可得,S2+
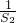 =a2-2=S2-a1-2,∴
=a2-2=S2-a1-2,∴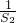 =
= -2,∴S2=-
-2,∴S2=- .
.同理可求得 S3=-
 ,S4=-
,S4=- .
.(2)猜想Sn =-
 ,n∈N+,下边用数学归纳法证明:
,n∈N+,下边用数学归纳法证明:①当n=2时,S2=a1+a2=-
 ,猜想成立.
,猜想成立.②假设当n=k时猜想成立,即SK=-
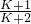 .
.则当n=k+1时,∵Sn+
 =an-2,∴
=an-2,∴ ,
,∴
 ,∴
,∴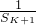 =
=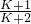 -2=
-2=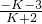 ,
,∴SK+1=-
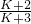 ,∴当n=k+1时,猜想仍然成立.
,∴当n=k+1时,猜想仍然成立.综合①②可得,猜想对任意正整数都成立,即 Sn =-
 ,n∈N+成立.
,n∈N+成立.分析:(1)S1=a1,由S2+
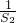 =a2-2=S2-a1 求得S2,同理求得 S3,S4.
=a2-2=S2-a1 求得S2,同理求得 S3,S4.(2)猜想Sn =-
 ,n∈N+,用数学归纳法证明,检验n=1时,猜想成立;假设SK=-
,n∈N+,用数学归纳法证明,检验n=1时,猜想成立;假设SK=-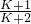 ,则当n=k+1时,由条件可得,
,则当n=k+1时,由条件可得, ,解出 SK+1=-
,解出 SK+1=-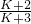 ,故n=k+1时,猜想仍然成立.
,故n=k+1时,猜想仍然成立.点评:本题考查归纳推理,用数学归纳法证明等式,证明当n=k+1时,Sn =-
 ,n∈N+,是解题的难点.
,n∈N+,是解题的难点. 
练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |