题目内容
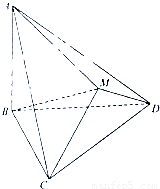
 如图△BCD与△MCD都是边长为2的正三角形,平面MCD
如图△BCD与△MCD都是边长为2的正三角形,平面MCD![]() 平面BCD,AB
平面BCD,AB![]() 平面BCD,
平面BCD,![]() 。
。
(1)求点A到平面MBC的距离;
(2)求平面ACM与平面BCD所成二面角的正弦值
取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD,又平面![]() 平面
平面![]() ,则MO⊥平面
,则MO⊥平面![]() .
.
以O为原点,直线OC、BO、OM为x轴,y轴,z轴,建立空间直角坐标系如图.
OB=OM=![]() ,则各点坐标分别为O(0,0,0),C(1,0,0),M(0,0,
,则各点坐标分别为O(0,0,0),C(1,0,0),M(0,0,![]() ),B(0,-
),B(0,-![]() ,0),A(0,-
,0),A(0,-![]() ,2
,2![]() ),
),
(1)设![]() 是平面MBC的法向量,则
是平面MBC的法向量,则![]() ,
,
![]() ,由
,由![]() 得
得![]() ;由
;由![]() 得
得![]() ;取
;取![]() ,则距离
,则距离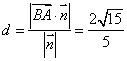
(2)![]() ,
,![]() .
.
![]()
![]() 设平面ACM的法向量为
设平面ACM的法向量为![]() ,由
,由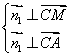 得
得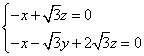 .解得
.解得![]() ,
,![]() ,取
,取![]() .又平面BCD的法向量为
.又平面BCD的法向量为![]() ,则
,则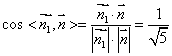
设所求二面角为![]() ,则
,则![]()

练习册系列答案
相关题目
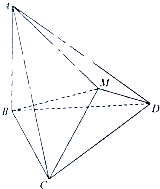 如图△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,
如图△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,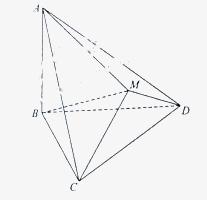 求点A到平面MBC的距离;
求点A到平面MBC的距离;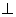 平面BCD,AB
平面BCD,AB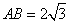 。
。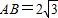 .
.