题目内容
已知数列{an}为等差数列,其前n项和为Sn,且Sn=2n2-n,数列{bn}是各项都为正数的等比数列,且b1=1,b1+b2+b3=13.
(1)求a3及数列{bn}的通项公式;
(2)设数列{bn}的前n项和为Tn,试求满足Tn≤a31的n的集合.
(1)求a3及数列{bn}的通项公式;
(2)设数列{bn}的前n项和为Tn,试求满足Tn≤a31的n的集合.
分析:(1)利用Sn=2n2-n,通过a3=S3-S2,求a3,设出公比利用b1+b2+b3=13,求出公比即可求解数列{bn}的通项公式;
(2)求出a31的值,求出数列{bn}的前n项和Tn,利用Tn≤a31得到n的不等式,求出n的集合.
(2)求出a31的值,求出数列{bn}的前n项和Tn,利用Tn≤a31得到n的不等式,求出n的集合.
解答:解:(1)因为Sn=2n2-n,所以a3=S3-S2=2×32-3-(2×22-2)=9…(2分)
依题意设等比数列{bn}的公比为q (q>0),由b1=1,b1+b2+b3=13得:1+q+q2=13,
即q2+q-12=0,解得q=3或q=-4,…(4分)
因为q>0,所以q=3,所以bn=3n-1…(6分)
(2)a31=S31-S30=2×312-31-(2×302-30)=121…(8分)
Tn=
=
,…(10分)
由Tn≤a31得:
≤121,
所以3n≤243=35,所以n≤5,…(12分)
又因为n∈N*,所以n=1,2,3,4,5;…(13分)
所以满足Tn≤a31的n的集合为{1,2,3,4,5}.…(14分)
依题意设等比数列{bn}的公比为q (q>0),由b1=1,b1+b2+b3=13得:1+q+q2=13,
即q2+q-12=0,解得q=3或q=-4,…(4分)
因为q>0,所以q=3,所以bn=3n-1…(6分)
(2)a31=S31-S30=2×312-31-(2×302-30)=121…(8分)
Tn=
| 1-3n |
| 1-3 |
| 3n-1 |
| 2 |
由Tn≤a31得:
| 3n-1 |
| 2 |
所以3n≤243=35,所以n≤5,…(12分)
又因为n∈N*,所以n=1,2,3,4,5;…(13分)
所以满足Tn≤a31的n的集合为{1,2,3,4,5}.…(14分)
点评:本题考查数列与不等式的综合,考查数列通项公式的求解,不等式的解法,考查转化思想,计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
定义:在数列{an}中,an>0且an≠1,若
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009=( )
| a | an+1 n |
| A、6026 | B、6024 |
| C、2 | D、4 |

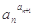 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4