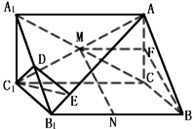
题目内容
如图,直三棱柱ABC﹣A1B1C1的底面积是等腰直角三角形,∠A1C1B1=90°,A1C1=1,
AA1= ,N、M分别是线段B1B、AC1的中点.
,N、M分别是线段B1B、AC1的中点.
(I)证明:MN∥平面ABC;
(II)求A1到平面AB1C1的距离
(III)求二面角A1﹣AB1﹣C1的大小.
AA1=
 ,N、M分别是线段B1B、AC1的中点.
,N、M分别是线段B1B、AC1的中点.(I)证明:MN∥平面ABC;
(II)求A1到平面AB1C1的距离
(III)求二面角A1﹣AB1﹣C1的大小.

解:(I)证明:取AC中点F,连接MF,BF,
在三角形AC1C中,MN∥C1C且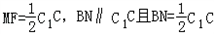 ,
,
∴MF∥BN且MF=BN
∴四边形MNBF为平行四边形
∴BF∥MN
∵BF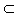 平面ABC
平面ABC
MN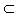 平面ABC不成立
平面ABC不成立
∴MN∥平面ABC
(II)设A1到平面AB1C1的距离为h,AA1⊥平面A1B1C1
∴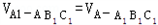
∴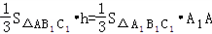
∵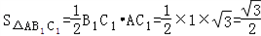 ,
,
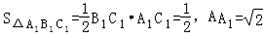
∴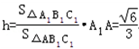
(III)三棱柱ABC﹣A1B1C1是直三棱柱,平面ABB1A1⊥平面A1B1C1,
又点D是等腰直角三角形A1B1C1斜边A1B1的中点.则C1D⊥A1B1
所以,C1D⊥平面A1B1BA;
平面A1B1BA内,过D作DE⊥AB1,垂足为E,连接C1E,则C1E⊥AB1;
∴∠C1ED是二面角,A1﹣AB1﹣C1的平面角,
在Rt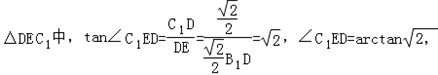
所以,二面角,A1﹣AB1﹣C1的大小为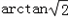 .
.
在三角形AC1C中,MN∥C1C且
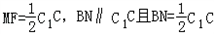 ,
,∴MF∥BN且MF=BN
∴四边形MNBF为平行四边形
∴BF∥MN
∵BF
 平面ABC
平面ABCMN
 平面ABC不成立
平面ABC不成立∴MN∥平面ABC
(II)设A1到平面AB1C1的距离为h,AA1⊥平面A1B1C1
∴
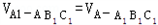
∴
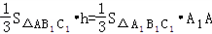
∵
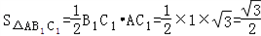 ,
,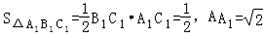
∴
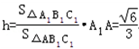
(III)三棱柱ABC﹣A1B1C1是直三棱柱,平面ABB1A1⊥平面A1B1C1,
又点D是等腰直角三角形A1B1C1斜边A1B1的中点.则C1D⊥A1B1
所以,C1D⊥平面A1B1BA;
平面A1B1BA内,过D作DE⊥AB1,垂足为E,连接C1E,则C1E⊥AB1;
∴∠C1ED是二面角,A1﹣AB1﹣C1的平面角,
在Rt
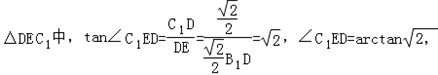
所以,二面角,A1﹣AB1﹣C1的大小为
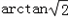 .
.

练习册系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.