题目内容
设数列{an}的前n项和为Sn,已知a1=1,且an+2SnSn-1=0(n≥2),(1)求数列{Sn}的通项公式;
(2)设Sn=
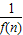 ,bn=f(
,bn=f(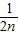 )+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn<
)+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn< .
.
【答案】分析:(1)利用数列递推式,再写一式,两式相减,可得数列{Sn}的通项公式;
(2)确定数列的通项,利用裂项法求数列的和,即可得到结论.
解答:(1)解:∵an+2SnSn-1=0(n≥2),
∴Sn-Sn-1+2SnSn-1=0.---------(3分)
∴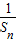 -
-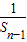 =2.
=2.
又∵a1=1,---------------(5分)
∴Sn=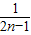 (n∈N+).---------------(7分)
(n∈N+).---------------(7分)
(2)证明:∵Sn=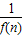 ,∴f(n)=2n-1.--------------------------(8分)
,∴f(n)=2n-1.--------------------------(8分)
∴bn=2(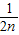 )-1+1=(
)-1+1=( )n-1.---------------------------------------(9分)
)n-1.---------------------------------------(9分)
Tn=( )•(
)•( )1+(
)1+( )1•(
)1•( )2+…+(
)2+…+( )n-1•(
)n-1•( )n=(
)n=( )1+(
)1+( )3+(
)3+( )5+…+(
)5+…+( )2n-1
)2n-1
= [1-(
[1-( )n].-------------------------------------------------------(11分)
)n].-------------------------------------------------------(11分)
∴Pn=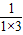 +
+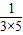 +…+
+…+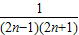 ---------------(13分)
---------------(13分)
=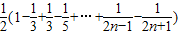 =
=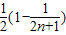 -------------------------------(14分)
-------------------------------(14分)
点评:本题考查数列递推式,考查数列的通项与求和,考查学生分析解决问题的能力,属于中档题.
(2)确定数列的通项,利用裂项法求数列的和,即可得到结论.
解答:(1)解:∵an+2SnSn-1=0(n≥2),
∴Sn-Sn-1+2SnSn-1=0.---------(3分)
∴
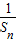 -
-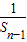 =2.
=2.又∵a1=1,---------------(5分)
∴Sn=
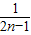 (n∈N+).---------------(7分)
(n∈N+).---------------(7分)(2)证明:∵Sn=
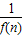 ,∴f(n)=2n-1.--------------------------(8分)
,∴f(n)=2n-1.--------------------------(8分)∴bn=2(
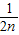 )-1+1=(
)-1+1=( )n-1.---------------------------------------(9分)
)n-1.---------------------------------------(9分)Tn=(
 )•(
)•( )1+(
)1+( )1•(
)1•( )2+…+(
)2+…+( )n-1•(
)n-1•( )n=(
)n=( )1+(
)1+( )3+(
)3+( )5+…+(
)5+…+( )2n-1
)2n-1=
 [1-(
[1-( )n].-------------------------------------------------------(11分)
)n].-------------------------------------------------------(11分)∴Pn=
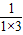 +
+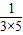 +…+
+…+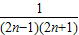 ---------------(13分)
---------------(13分)=
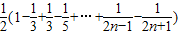 =
=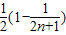 -------------------------------(14分)
-------------------------------(14分)点评:本题考查数列递推式,考查数列的通项与求和,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目