题目内容
在正方体ABCD-A1B1C1D1中，P、Q分别是棱AA1、CC1的中点，则过点B、P、Q的截面是（ ）A．三角形
B．菱形但不是正方形
C．正方形
D．邻边不等的矩形
【答案】分析：先由共面公理证明四点P、B、Q、D1共面，再证明其是一个菱形即可．
解答：解：如图所示：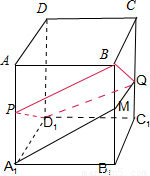
连接PD1、QD1．下面证明四边形BPD1Q是菱形．
取棱BB1的中点M，连接A1M、QM，则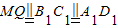
，
∴四边形A1MQD1是平行四边形，∴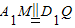
；
同理可证：四边形A1MQP是一个平行四边形，∴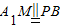
，
∴
，
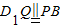∴四边形PBQD1是平行四边形．
由Rt△ABP≌Rt△A1D1P，可得PB=PD1．
∴四边形PBQD1是菱形．
故选B
点评：熟练掌握共面公理和菱形的定义及三角形全等是解题的关键．
解答：解：如图所示：
连接PD1、QD1．下面证明四边形BPD1Q是菱形．
取棱BB1的中点M，连接A1M、QM，则
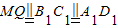，∴四边形A1MQD1是平行四边形，∴
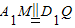；同理可证：四边形A1MQP是一个平行四边形，∴
，∴
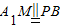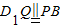，∴四边形PBQD1是平行四边形．
由Rt△ABP≌Rt△A1D1P，可得PB=PD1．
∴四边形PBQD1是菱形．
故选B
点评：熟练掌握共面公理和菱形的定义及三角形全等是解题的关键．
练习册系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）