题目内容
如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB．
（I）求证：CE⊥平面PAD；
（II）若PA=AB=1，AD=3，CD=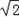
，∠CDA=45°，求四棱锥P-ABCD的体积．
（I）求证：CE⊥平面PAD；
（II）若PA=AB=1，AD=3，CD=
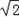，∠CDA=45°，求四棱锥P-ABCD的体积．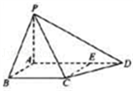
解：（I）证明：∵PA⊥平面ABCD，CE
平面ABCD，
∴PA⊥CE，
∵AB⊥AD，CE∥AB，
∴CE⊥AD又PA∩AD=A，
∴CE⊥平面PAD
（II）由（I）可知CE⊥AD在Rt△ECD中，DE=CDcos45°=1，CE=CDsin45°=1，
又∵AB=CE=1，AB∥CE
∴四边形ABCE为矩形
∴
=
又PA平面ABCD，PA=1
∴
平面ABCD，∴PA⊥CE，
∵AB⊥AD，CE∥AB，
∴CE⊥AD又PA∩AD=A，
∴CE⊥平面PAD
（II）由（I）可知CE⊥AD在Rt△ECD中，DE=CDcos45°=1，CE=CDsin45°=1，
又∵AB=CE=1，AB∥CE
∴四边形ABCE为矩形
∴
=又PA平面ABCD，PA=1
∴
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD，PA⊥平面ABCD，ABCD是直角梯形，DA⊥AB，CB⊥AB，PA=2AD=BC=2，AB=