题目内容
实数集A满足条件:若a∈A,则
∈A(a≠1).
求证:①若2∈A,则A中必还有另外两个元素;
②集合A不可能是单元素集.
| 1 |
| 1-a |
求证:①若2∈A,则A中必还有另外两个元素;
②集合A不可能是单元素集.
证明:①若a∈A,则
∈A.
又∵2∈A,
∴
=-1∈A
∵-1∈A,∴
=
∈A.
∵
∈A,∴
=2∈A.
∴A中另外两个元素为-1,
②若A为单元素集,则a=
,即a2-a+1=0,方程无解.
∴a≠
,
∴A不可能为单元素集.
| 1 |
| 1-a |
又∵2∈A,
∴
| 1 |
| 1-2 |
∵-1∈A,∴
| 1 |
| 1-(-1) |
| 1 |
| 2 |
∵
| 1 |
| 2 |
| 1 | ||
1-
|
∴A中另外两个元素为-1,
| 1 |
| 2 |
②若A为单元素集,则a=
| 1 |
| 1-a |
∴a≠
| 1 |
| 1-a |
∴A不可能为单元素集.

练习册系列答案
相关题目
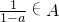 (a≠1).
(a≠1).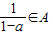 (a≠1).
(a≠1).