题目内容
已知椭圆C1: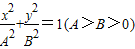 和双曲线C2:
和双曲线C2: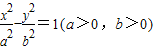 有相同的焦点F1、F2,2c是它们的共同焦距,且它们的离心率互为倒数,P是它们在第一象限的交点,当cos∠F1PF2=60°时,下列结论中正确的是( )
有相同的焦点F1、F2,2c是它们的共同焦距,且它们的离心率互为倒数,P是它们在第一象限的交点,当cos∠F1PF2=60°时,下列结论中正确的是( )A.c4+3a4=4a2c2
B.3c4+a4=4a2c2
C.c4+3a4=6a2c2
D.3c4+a4=6a2c2
【答案】分析:利用椭圆、双曲线的定义,结合余弦定理,可得4c2=A2+3a2,利用离心率互为倒数,可得A= ,由此可得结论.
,由此可得结论.
解答:解:由题意,|PF1|+|PF2|=2A,|PF1|-|PF2|=2a,则|PF1|=A+a,|PF2|=A-a
∵cos∠F1PF2=60°,∴4c2=(A+a)2+(A-a)2-(A+a)(A-a)=A2+3a2,
∵离心率互为倒数
∴ =1
=1
∴A=
∴4c2= +3a2,
+3a2,
∴c4+3a4=4a2c2,
故选A.
点评:本题考查椭圆、双曲线的定义与几何性质,考查余弦定理,属于中档题.
 ,由此可得结论.
,由此可得结论.解答:解:由题意,|PF1|+|PF2|=2A,|PF1|-|PF2|=2a,则|PF1|=A+a,|PF2|=A-a
∵cos∠F1PF2=60°,∴4c2=(A+a)2+(A-a)2-(A+a)(A-a)=A2+3a2,
∵离心率互为倒数
∴
 =1
=1∴A=

∴4c2=
 +3a2,
+3a2,∴c4+3a4=4a2c2,
故选A.
点评:本题考查椭圆、双曲线的定义与几何性质,考查余弦定理,属于中档题.

练习册系列答案
相关题目
 与双曲线C2:
与双曲线C2: 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点,C1恰好将线段AB三等分,则( )
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点,C1恰好将线段AB三等分,则( ) B.
B. C.
C. D.
D.
 与双曲线C2:
与双曲线C2: 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点.若C1恰好将线段
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点.若C1恰好将线段 三等分,则( )
三等分,则( ) B.
B. C.
C. D.
D.
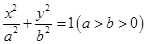 与双曲线C2:
与双曲线C2: 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点.若C1恰好将线段
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点.若C1恰好将线段 三等分,则( )
三等分,则( ) B.
B. C.
C. D.
D.
 和双曲线C2:
和双曲线C2: 有相同的焦点F1、F2,2c是它们的共同焦距,且它们的离心率互为倒数,P是它们在第一象限的交点,当cos∠F1PF2=60°时,下列结论中正确的是
有相同的焦点F1、F2,2c是它们的共同焦距,且它们的离心率互为倒数,P是它们在第一象限的交点,当cos∠F1PF2=60°时,下列结论中正确的是