题目内容
(本小题满分12分)已知圆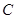 的圆心为原点,且与直线
的圆心为原点,且与直线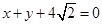 相切。
相切。
(1)求圆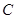 的方程;
的方程;
(2)点 在直线
在直线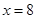 上,过
上,过 点引圆
点引圆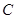 的两条切线
的两条切线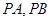 ,切点为
,切点为 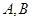 ,求证:直线
,求证:直线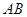 恒过定点。
恒过定点。

【答案】
解:(1)依题意得:圆 的半径
的半径 ,所以圆
,所以圆 的方程为
的方程为 。(4分)
。(4分)
(2) 是圆
是圆 的两条切线,
的两条切线, 。
。 在以
在以 为直径的圆上。
为直径的圆上。
设点 的坐标为
的坐标为 ,则线段
,则线段 的中点坐标为
的中点坐标为 。
。
 以
以 为直径的圆方程为
为直径的圆方程为 (8分)
(8分)
化简得:
 为两圆的公共弦,
为两圆的公共弦,
 直线
直线 的方程为
的方程为
所以直线 恒过定点
恒过定点 。(12分)
。(12分)
【解析】略

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目