题目内容
 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为
- A.

- B.
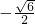
- C.

- D.

D
分析:由f(x)=Acos(ωx+φ)为奇函数,利用奇函数的性质可得f(0)=Acosφ=0结合已知0<φ<π,可求 φ=
再由△EFG是边长为2的等边三角形,可得 =A,结合图象可得,函数的周期 T=4,根据周期公式可得,ω,从而可得f(x),代入可求f(1).
=A,结合图象可得,函数的周期 T=4,根据周期公式可得,ω,从而可得f(x),代入可求f(1).
解答:∵f(x)=Acos(ωx+φ)为奇函数
∴f(0)=Acosφ=0
∵0<φ<π∴φ=
∴f(x)=Acos(ωx )=-Asinωx
)=-Asinωx
∵△EFG是边长为2的等边三角形,则 =A
=A
又∵函数的周期 T=2FG=4,根据周期公式可得,ω=
∴f(x)=-Asin x=
x=
则f(1)=
故选D
点评:本题中的重要性质要注意灵活运用:若奇函数的定义域包括0,则f(0)=0;解决本题的另一关键是要由△EFG是边长为2的等边三角形,及三角形与函数图象之间的关系得到 =A,这也是本题的难点所在.
=A,这也是本题的难点所在.
分析:由f(x)=Acos(ωx+φ)为奇函数,利用奇函数的性质可得f(0)=Acosφ=0结合已知0<φ<π,可求 φ=

再由△EFG是边长为2的等边三角形,可得
 =A,结合图象可得,函数的周期 T=4,根据周期公式可得,ω,从而可得f(x),代入可求f(1).
=A,结合图象可得,函数的周期 T=4,根据周期公式可得,ω,从而可得f(x),代入可求f(1).解答:∵f(x)=Acos(ωx+φ)为奇函数
∴f(0)=Acosφ=0
∵0<φ<π∴φ=

∴f(x)=Acos(ωx
 )=-Asinωx
)=-Asinωx ∵△EFG是边长为2的等边三角形,则
 =A
=A又∵函数的周期 T=2FG=4,根据周期公式可得,ω=

∴f(x)=-Asin
 x=
x=
则f(1)=

故选D
点评:本题中的重要性质要注意灵活运用:若奇函数的定义域包括0,则f(0)=0;解决本题的另一关键是要由△EFG是边长为2的等边三角形,及三角形与函数图象之间的关系得到
 =A,这也是本题的难点所在.
=A,这也是本题的难点所在. 
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目