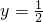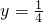题目内容
过圆x2+y2=1外一点P作圆的两条切线,当两条切线互相垂直时,点P的轨迹方程是_____________.
答案：x2+y2=2
解析:圆x2+y2=1,圆心O(0,0),半径为1,由题可知|PO|=
.
则P的轨迹是以O(0,0)为圆心,
为半径的圆:x2+y2=2.
练习册系列答案
相关题目
过圆x2+y2=1外一点（0，4）作圆的两条切线，切点分别是A、B，则弦AB所在直线方程是（ ）
A、y=
| ||
B、y=
| ||
C、x=
| ||
D、x=
|
过圆x2+y2=4外一点P（4，2）作圆的两条切线，切点分别为A，B，则△ABP的外接圆方程是（ ）
| A、（x-4）2+（y-2）2=1 | B、x2+（y-2）2=4 | C、（x+2）2+（y+1）2=5 | D、（x-2）2+（y-1）2=5 |
